Characteristic

The term "characteristic" has many different uses in mathematics. In general, it refers to some property that inherently describes a given mathematical object, for example characteristic class, characteristic equation, characteristic factor, etc. However, the unqualified term "characteristic" also has a number of specific meanings depending on context.

For a real number 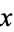,  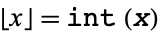is called the characteristic, where  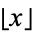is the floor function.

A path in a two-dimensional plane used to transform partial differential equations into systems of ordinary differential equations is also called a characteristic. This form of characteristic was invented by Riemann. For an example of the use of characteristics, consider the equation

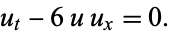Now let 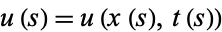. Since

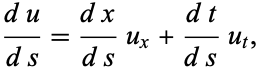it follows that 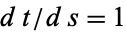, , 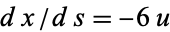and 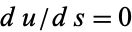. Integrating gives 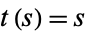, , 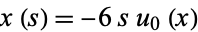and 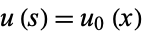, where the constants of integration are 0 and .

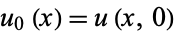REFERENCES:

Farlow, S. J. Partial Differential Equations for Scientists and Engineers. New York: Dover, pp. 205-212, 1993.

Landau, L. D. and Lifschitz, E. M. Fluid Mechanics, 2nd ed. Oxford, England: Pergamon Press, pp. 310-346, 1982.

Moon, P. and Spencer, D. E. Partial Differential Equations. Lexington, MA: Heath, pp. 27-29, 1969.

Whitham, G. B. Linear and Nonlinear Waves. New York: Wiley, pp. 113-142, 1974.

Zauderer, E. Partial Differential Equations of Applied Mathematics, 2nd ed. New York: Wiley, pp. 78-121, 1989.

Zwillinger, D. "Method of Characteristics." §88 in Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 325-330, 1997.