


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-6-2018
Date: 30-5-2018
Date: 3-7-2018
|
The second-order ordinary differential equation
![(d^2y)/(dx^2)+[theta_0+2sum_(n=1)^inftytheta_ncos(2nx)]y=0,](http://mathworld.wolfram.com/images/equations/HillsDifferentialEquation/NumberedEquation1.gif) |
(1) |
where 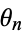 are fixed constants. A general solution can be given by taking the "determinant" of an infinite matrix.
are fixed constants. A general solution can be given by taking the "determinant" of an infinite matrix.
If only the 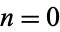 term is present, the equation have solution
term is present, the equation have solution
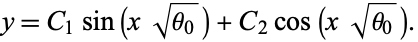 |
(2) |
If terms 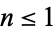 are included, the equation becomes the Mathieu differential equation, which has solution
are included, the equation becomes the Mathieu differential equation, which has solution
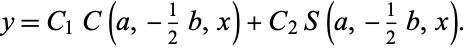 |
(3) |
If terms 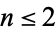 are included, it becomes the Whittaker-Hill differential equation.
are included, it becomes the Whittaker-Hill differential equation.
REFERENCES:
Hill, G. W. "On the Part of the Motion of Lunar Perigee Which is a Function of the Mean Motions of the Sun and Moon." Acta Math. 8, 1-36, 1886.
Ince, E. L. Ordinary Differential Equations. New York: Dover, p. 384, 1956.
Magnus, W. and Winkler, S. Hill's Equation. New York: Dover, 1979.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 123, 1997.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|