


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-8-2019
Date: 17-9-2018
Date: 22-8-2019
|
A real-valued univariate function 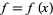 is said to have a removable discontinuity at a point
is said to have a removable discontinuity at a point 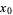 in its domain provided that both
in its domain provided that both 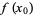 and
and
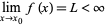 |
(1)
|
exist while 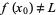 . Removable discontinuities are so named because one can "remove" this point of discontinuity by defining an almost everywhere identical function
. Removable discontinuities are so named because one can "remove" this point of discontinuity by defining an almost everywhere identical function 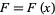 of the form
of the form
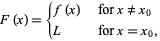 |
(2)
|
which necessarily is everywhere-continuous.
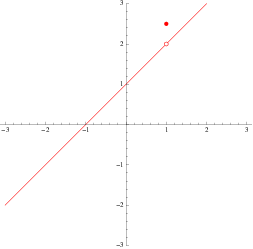
The figure above shows the piecewise function
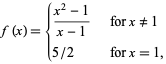 |
(3)
|
a function for which 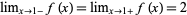 while
while 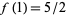 . In particular,
. In particular, 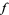 has a removable discontinuity at
has a removable discontinuity at 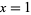 due to the fact that defining a function
due to the fact that defining a function 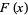 as discussed above and satisfying
as discussed above and satisfying 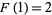 would yield an everywhere-continuous version of
would yield an everywhere-continuous version of 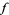 .
.
Note that the given definition of removable discontinuity fails to apply to functions 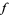 for which
for which 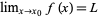 and for which
and for which 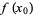 fails to exist; in particular, the above definition allows one only to talk about a function being discontinuous at points for which it is defined. This definition isn't uniform, however, and as a result, some authors claim that, e.g.,
fails to exist; in particular, the above definition allows one only to talk about a function being discontinuous at points for which it is defined. This definition isn't uniform, however, and as a result, some authors claim that, e.g., 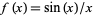 has a removable discontinuity at the point
has a removable discontinuity at the point 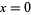 . This notion is related to the so-called sinc function.
. This notion is related to the so-called sinc function.
Among real-valued univariate functions, removable discontinuities are considered "less severe" than either jump or infinite discontinuities.
Unsurprisingly, one can extend the above definition in such a way as to allow the description of removable discontinuities for multivariate functions as well.
Removable discontinuities are strongly related to the notion of removable singularities
This entry contributed by Christopher Stover



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|