العنوان:تحليل الاستقرارية والحل العددي لمعادلة Huxley

 اسم الباحث: محمد عبد محيميد سالم السبعاوي   

الجامعه والكليه:  كلية علوم الحاسبات والرياضيات في جامعة الموصل

الخلاصه :

لقد تمت دراسة استقرارية الحلول اللازمنية (Steady State Solutions) لمعادلةHuxley      باستخدام   طريقة   تحليل   الاستقرارية   من   النمط     Fourier Analysis) (Fourier Mode Stability  في حالتين: الأولى في حالة كون السعة A ثابتة والثانية في حالة كون السعة A متغيرة إذ تم استخدام طريقة Galerkin العددية مع الحل التحليلي في هذه الحالة. وقد تبين في كلتا الحالتين أن الحلين اللازمنيين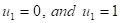and 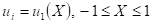  مستقران   دوماً  في  حين  أن  الحلين 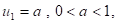 مستقران على نحو مشروط كما تم في الحالة الثانية مقارنة النتائج التحليلية لدراسة الاستقرارية بالحل العددي لطريقة Galerkin وقد تم الحصول على النتائج نفسها. كذلك تم حل  معادلة  Huxley   عددياً   باستخدام   طريقتين   من   طرائق    الفروقات   المنتهية (Finite Difference Methods) : الأولى هي الطريقة الصريحة (Explicit Scheme) والثانية هي طريقة Crank-Nicholson إذ تم عمل مقارنة بين نتائج كلتا الطريقتين وقد تبين أن الطريقة الأولى هي الأسهل والأسرع تقارباً في حين كانت الطريقة الثانية هي الأدق ولقد تمت كذلك دراسة استقرارية كلتا الطريقتين باستخدام طريقة Fourier (von Neumann) إذ تبين أن الطريقة الأولى مستقرة على نحو مشروط (Conditionally Stable) إذا كان  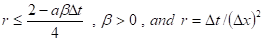  في حين كانت الطريقة الثانية مستقرة على نحو غير مشروط (Unconditionally Stable).

         The stability analysis of steady state solutions of Huxley equation using Fourier mode stability analysis in two cases has been considered: Firstly when the amplitude A is constant and secondly when the amplitude A is variable. In the two cases the results found to be: The steady state solutions 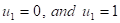 are always stable while the solutions 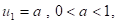and 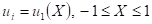 are conditionally stable. In the second case the comparison between the analytical solution and the numerical solution of Galerkin technique has been done. This comparison showed that the analytical solution and the numerical solution of Galerkin technique are the same. Also, the numerical solution of Huxley equation has been done using two finite difference methods: The explicit scheme and Crank-Nicholson scheme. The results of the comparison between the two methods found to be: The first scheme is simpler and has faster convergence while the second scheme is more accurate. Also, the stability analysis of the two methods by the use of Fourier (von Neumann) method has been done and the results found to be: the explicit scheme is conditionally stable if  and Crank-Nicholson scheme is unconditionally stable.

ملاحظه: للحصول على الملف كاملا يمكنكم مراسلتنا عل البريد الالكتروني 

(almerjamathematics@gmail.com)