العنوان: توسيع خوارزميات التدرج المترافق لحل
 مسائل الأمثلية غير المقيدة

 

 اسم الباحث:    عدي سالم نوح شكوري

الجامعه والكليه:  كلية علوم الحاسبات والرياضيات في جامعة الموصل

الخلاصه :

في هذه الرسالة تم توسيع واستخدام عدد من الخوارزميات الجديدة في مجال التدرج المترافق لحل المسائل في الامثلية غير المقيدة .

 

حيث تم الاستفادة من تقنية شريحة الوصل التكعيبية (Cubic Spline) في دمجها مع تقنية الاستكمال التكعيبي (Cubic Interpolation) والحصول على خوارزمية جديدة لإيجاد القيمة الصغرى للدالة الأحادية ، كما تم اقتراح نموذجاً اكثر عمومية من النماذج التربيعية لحل المسائل في الامثلية اللاخطية هو نموذج الدالة الآسية غير التربيعية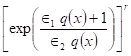 حيث أن q(x) دالة تربيعية ،هذه الخوارزمية المقترحة هي اكثر ملائمة من الخوارزمية التقليدية التي تعتمد على الدالة التربيعية فقط وإنها مازالت تحافظ على خاصية التوقف التربيعي ، كما تم التعرف على صيغة مطورة (وغير معروفة كثيراً)  للتدرج المترافق والاستفادة من هذه الصيغة من خلال إجراء تداخل (Interleave) بينها وبين صيغة Fletcher وقد قورنت هذه الصيغة مع الصيغ الأخرى وبينت كفاءتها .

 

ومن خلال المقارنة العددية مع الطرائق التقليدية من نوع CG لوحظ بان النتائج العددية بشكل إجمالي تشير إلى كفاءة الخوارزميات المقترحة في هذه الرسالة وباستعمال عدد معين من الدوال اللاخطية الاختيارية المعروفة .

In this thesis we have extended and used a number of new algorithms in the field of the conjugate gradient for solving unconstrained optimization problems.

  

We make use of the Cubic Spline technique by mixing it with the Cubic Interpolation technique to get a new algorithm for finding the minimum value for the unimodal function , Also we  suggest more general model than quadratic once for solving nonlinear optimization problems which modify the classical conjugate gradient methods, this suggested model can be expressed in the form of the non quadratic exponential function 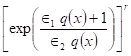where q(x) is a quadratic function . This suggestion algorithm is more suitable algorithm than the classical once which depends on the quadratic function only and this algorithm still preserve on the quadratic termination property .

Also, we make use of a new developed Conjugate Gradient formula (not known) by making interleave between it and Fletcher Reeves formula . 

 

We note from the numerical comparison, that the suggestion algorithms in this thesis are more efficient than the standard CG-methods for solving some variety of nonlinear standard test functions.

 

ملاحظه: للحصول على الملف كاملا يمكنكم مراسلتنا عل البريد الالكتروني 

(almerjamathematics@gmail.com)

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يقيم مسابقة الكوثر الخاصة بترتيل القرآن الكريم في كربلاء

قسم الشؤون الفكرية والثقافية يُصدر العدد الثالث والعشرين من مجلّة (أوراق معرفية)

قسم التربية والتعليم يُطلق الموسم التدريبيّ الصيفيّ لملاكات مجموعة العميد التربوية

المجمَع العلمي يُطلق المرحلة الثالثة من مشروع أمير القرّاء الوطني

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد

مواضيع ذات صلة

الحلول العددية للمعادلات التباطؤية الاعتيادية ذات التباطؤ الصغير باستخدام الطرائق متعددة الخطوات

الحلول العددية للمعادلات التفاضلية الكسرية

حل المعادلات ذات البعدين (التكاملية و التكاملية-التفاضلية)

بعض النتائج لدوال متعددة القيم فيما يختص بنظريات النقطة الصامدة وتكرارات ايشكاوا

حول مقارنة طرق التقدير لمعلمة ودالة البقاء للتوزيع الاسي باستخدام المحاكاة

حول مقاسات أولية كاذبة ومقاسات جزئية أولية كاذبة

تعميمات الـGCD-Domain من النوع a+xb[[x]] , a+xb[x]

الحلول الدورية لبعض أنظمة المعادلات التفاضلية اللاخطية ذات التأثير النبضي

خوارزميات هجينية لخوارزمية شبيهة نيوتن في الأمثلية ذات القياس الواسع

تحليل الاستقرارية والحل العددي لمعادلة Huxley

الخوارزميـــات القـــــــابلة للتوســـع فــــي الأمثليـــــــــة غير المقيدة ذات القيــــــاس العالي

حول الفضاءات التبولوجية المضببة الحدسية الخاصة