
Magnification bias
 المؤلف:
Heino Falcke and Friedrich W Hehl
المؤلف:
Heino Falcke and Friedrich W Hehl
 المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
 الجزء والصفحة:
p 270
الجزء والصفحة:
p 270
 6-2-2017
6-2-2017
 1842
1842
A lens magnifies by enlarging the angular size of the unlensed sky behind it, and since surface brightness is conserved, the fluxes of sources are magnified by the same amount. When the photometric sensitivity is such that all the stars can be detected even without being magnified, then the effect of lensing is to decrease the surface density of sources. However, if the fainter stars cannot be observed unless magnified, there are two possibilities: either there are enough faint sources that are magnified above the detection threshold to over-compensate for the decrease in surface density (‘positive magnification bias’), or there are not enough faint sources (‘negative magnification bias’). The lensed luminosity function (number of stars per flux interval) is related to the unlensed one by
 (1.1)
(1.1)
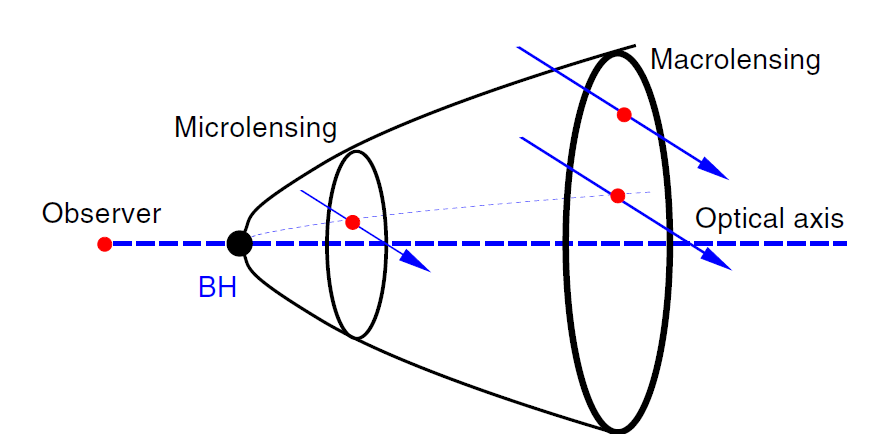
Figure 1.1. The lensing cross section, timescale and magnification as a function of source distance behind the MBH. The size of the Einstein ring, or lensing cross section, increases with distance behind the MBH. Close behind the MBH the Einstein ring (and the distance between the two images) is smaller than the telescope's angular resolution and the lensing appears as a microlensing event. Farther out, the Einstein ring is large enough for the two images to be resolved, and the lensing appears as a macro lensing event. The duration and peak magnification of the events depend on the impact parameter of the stellar trajectories (arrows). The closer they are to the optical axis, the longer the events and the higher the peak magnification are. Trajectories with impact parameters at a fixed ratio of the Einstein radius (the two trajectories connected by the dotted line) will have the same peak magnification, but the event duration will be longer for the sources farther away behind the MBH (assuming a uniform velocity field).
where Σ is the surface number density of stars and F the flux. In many cases the luminosity function is well approximated by a power law, dΣ/dF ∝ F −β. It then follows from equation (1.1) that for β = 2 the decrease in the total surface density is exactly balanced by the magnification of faint stars above the detection threshold.
The chances for the detection of this effect in the Galactic Center appear small. A statistically meaningful detection requires a very high surface density that probably exceeds even that around the MBH (Wardle and Yusef-Zadeh 1992), and furthermore, models of the stellar luminosity function in the inner Galactic Center suggests that β ∼ 2 for giants (Alexander and Sternberg 1999).
 الاكثر قراءة في مواضيع عامة في علم الفلك
الاكثر قراءة في مواضيع عامة في علم الفلك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


