


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-2-2017
Date: 22-12-2015
Date: 12-2-2017
|
Motion in the equatorial plane
For particles moving in the equatorial plane of a rotating black hole, the expressions for dr/dτ and dφ/dτ can be written in the form
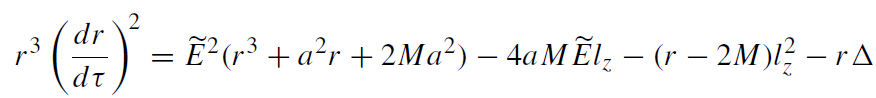 (1.1)
(1.1)
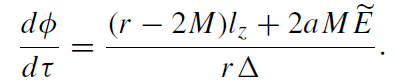 (1.2)
(1.2)
They are analogous to the corresponding equations for a Schwarzschild black hole. An analysis of the peculiarities of motion is performed in the same way as before by using the effective potential.
1.1 Circular orbits
The most important class of orbits is circular orbits. For given Ẽ and lz , the radius r0 of a circular orbit can be found by solving simultaneously the equations
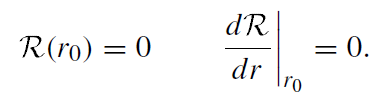 (1.3)
(1.3)
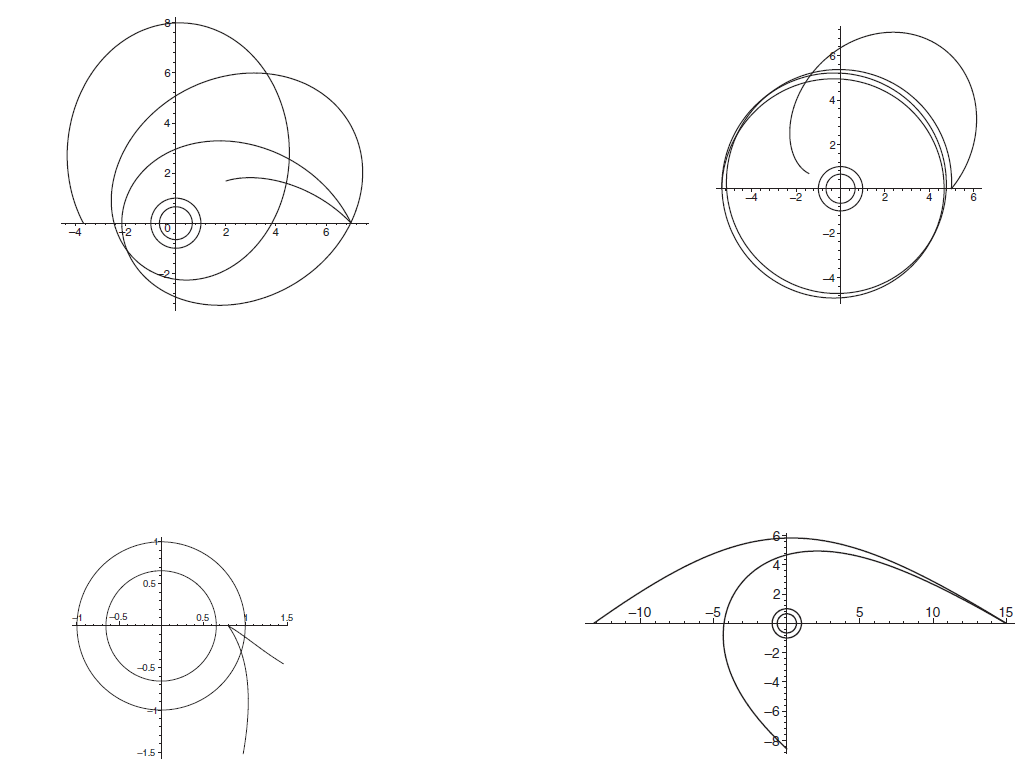
Figure 1.1. Trajectories of particles in the equatorial plane. In each case two trajectories are shown. Both trajectories have the same initial conditions. The particle is moving in the Kerr metric with a = |a| and a = −|a|, respectively.
One can also use these equations to obtain the expressions for the specific energy Ẽcirc and specific angular momentum lcirc as functions of the radius r of the circular motion [15],
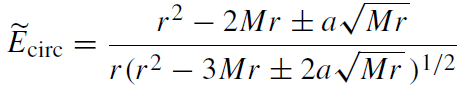 (1.4)
(1.4)
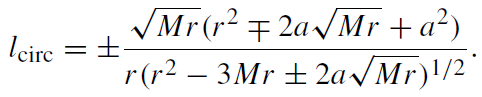 (1.5)
(1.5)
The upper signs in these and the subsequent formulas correspond to direct orbits (i.e. co-rotating with lz > 0), and the lower signs correspond to retrograde orbits (counter-rotating with lz < 0). We always assume that a ≥ 0.
The coordinate angular velocity of a particle on the circular orbit is
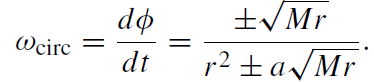 (1.6)
(1.6)
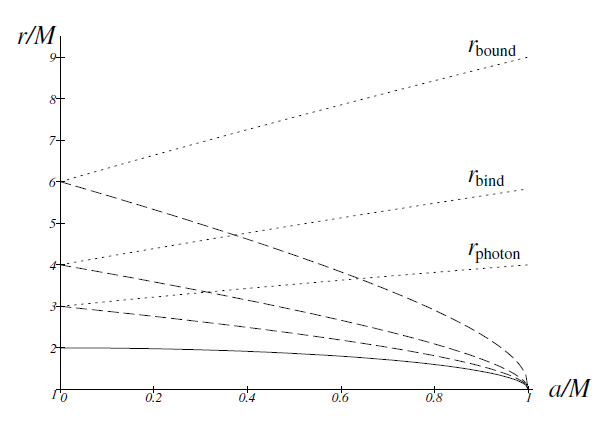
Figure 1.2. rphoton, rbind, and rbound as functions of the rotation parameter a/M. The quantities corresponding to the direct and retrograde motions are shown by dashed and dotted lines, respectively.
1.2 Last stable circular orbits
Circular orbits can exist only for those values of r for which the denominator in the expressions for Ẽcirc and lcirc is real, i.e.
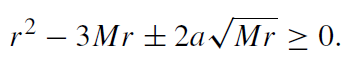 (1.7)
(1.7)
The radius of the circular orbit closest to the black hole (the motion along it occurs at the speed of light) is
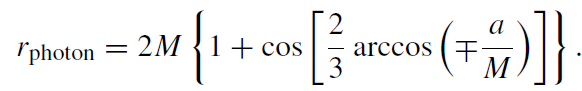 (1.8)
(1.8)
This orbit is unstable. For a = 0, we have rphoton = 3M, while for a = M, we
find rphoton = M (direct motion) or rphoton = 4M (retrograde motion).
The circular orbits with r > rphoton and Ẽ ≥ 1 are unstable. A small perturbation directed outwards forces the particle to leave its orbit and escape to infinity on an asymptotically hyperbolic trajectory.
The radius of the unstable circular orbit, on which Ẽcirc = 1, is given by
 (1.9)
(1.9)
These values of the radius are the minima of periastra of all parabolic orbits. A particle in the equatorial plane, coming from infinity where its velocity is v∞ << c, is captured if it passes the black hole closer than rbind.
Finally the radius of the boundary circle separating stable circular orbits from unstable ones is given by the expression
 (1.10)
(1.10)
Table 1.1. The radii rphoton, rbind, and rbound (in units of rS = 2M) for a non-rotating (a = 0) and an extremely rotating (a = M) black hole.

Table 1.2. Specific energy Ẽ, specific binding energy 1 − Ẽ, and specific angular momentum |lz |/M of a test particle at the last stable circular orbit.

where
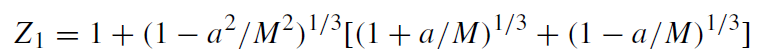 (1.11)
(1.11)
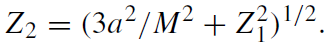 (1.12)
(1.12)
The quantities rphoton, rbind, and rbound as the functions of the rotation parameter a/M are shown in figure 1.2.
Table 1.1 lists rphoton, rbind, and rbound for the black hole rotating at the limiting angular velocity, a = M, and gives a comparison with the case of a = 0 (in units of rS = 2M). As a → M, the invariant distance from a point r to the horizon r+,
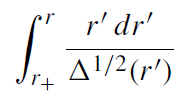 (1.13)
(1.13)
diverges. This does not mean that all orbits coincide in this limit and lie at the horizon, although at L > 0 the radii r of all three orbits tend to the same limit r+ [15]. Finally, we will give the values of specific energy Ẽ, specific binding energy 1 − Ẽ, and specific angular momentum |lz |/M of a test particle at the last stable circular orbit, rbound (see table 1.2).
The binding energy has a maximum for an extremely rotating black hole with a = M. It is equal to
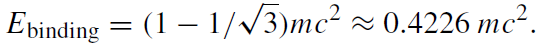 (1.14)
(1.14)
Thus, the maximum efficiency of the energy release by matter falling into a rotating black hole is 42%. This is much higher than in a non-rotating case.
1.3 Motion with negative Ẽ
It is easy to show that orbits with negative Ẽ are possible within the ergosphere for any θ ≠ 0, π. This follows from the fact that the Killing vector ξ(t) is spacelike inside the ergosphere. The specific energy Ẽ is defined as Ẽ = −uμξμ (t). Local analysis shows that for a fixed spacelike vector ξ(t) it is always possible to find a timelike or null vector uμ representing the four-velocity of a particle or a photon so that Ẽ is negative. Orbits with Ẽ < 0 make it possible to devise processes that extract the ‘rotational energy’ of the black hole. Such processes were discovered by Penrose [16].



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|