


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | INTRODUCTION TO PROBABILITY IN FINITE SAMPLE SPACES-Conditional probability |
|
|
|
Read More
Date: 9-1-2017
Date: 7-1-2017
Date: 25-12-2016
|
To introduce the concept of conditional probability, consider the following example. An urn contains 10 large marbles of which 6 are white and 4 are black, and 10 small marbles of which 3 are white and 7 are black. Let the event that a marble drawn at random is white be denoted by W, and that it is large be denoted by L.
It is clear that P(W) = 9/20 Suppose that a marble is drawn and it is large. The probability that it is also white is 5. The reason these values are different is that the first is based on a sample space with 20 points of which 9 correspond to white marbles, and the second is based on a sample space of 10 points of which 6 correspond to white marbles. The second probability will be referred to as the probability that the ball is white knowing it is large, and will be denoted by P(WIL). This intuitive ex- ample suggests the following definition.
DEFINITION. Let X be an event in an arbitrary sample space with nonzero probability, and let Y be any event in the same sample space. The conditional probability that Y occurs knowing that X has occurred is defined by

If both numerator and denominator of P(YIX) are divided by the number of points in the sample space, this formula becomes

Still another useful form for the formula is obtained by multiplying both sides of (2) by P(X). This gives
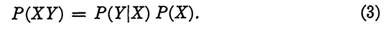
A final formula which is often useful comes as an application of Theorem 2 of (The number of elements in a set). Let Y be any event, and let X1, X 2, ... , Xm be events
representing disjoint sets (mutually exclusive) and such that
X1+X2+...+Xm= 1,
the entire sample space. Then it follows from Theorem 2 of (The number of elements in a set).
that P(Y) = P(YX1) + P(YX2) + + P(YXm), and applying (3) above, we obtain
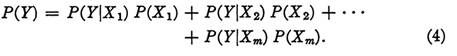
Example 1. Find the probability that a card dealt from a bridge deck is an ace, if it is known to be either an ace or a face card (that is, A, K, Q, or J).
Solution. Let Y denote the event that the card is an ace, and X the event that it is either an ace or a face card. The definition gives
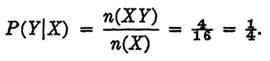
EXAMPLE 2. A certain group of students is two thirds males and one third females. Of these, one tenth of the males are color-blind. What is the probability that a student selected at random will be a color-blind male?
Solution. Let Y be the event that the student is color-blind, and X the event that he is male. Equation (3) gives
P(XY) = P(YI X) P(X) =(1/10) (2/3)=1/15
EXAMPLE 3. In a factory, three operators A, B, and C alternate in shifts in operating a certain machine. Records show that the number of parts produced by A, B, and C, respectively, are in the ratio 4:5:6. Of the parts produced, 1% of A's, 2% of B's, and 3% of C's are defective. What is the probability that a part drawn at random from the output of their machine will be defective?
Solution. Let D represent the event that the part is defective, and let A, B, and C represent the events that the part is produced by operator A, B, or C, respectively. Using Eq. (4), we find that
P(D) = P(DIA) P(A) + P(DIB) P(B) + P(DIC) P(C)
= 0.01 (4/15)+0.02(1/3)+0.03(2/5)
= 0.0213, approximately.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
خدمات متعددة يقدمها قسم الشؤون الخدمية للزائرين
|
|
|