We begin in this section with a quick introduction to some variational methods.

These ideas will later serve as motivation for the Pontryagin Maximum Principle.

Assume we are given a smooth function L : Rⁿ × Rⁿ → R, L = L(x, v); L is called the Lagrangian. Let T > 0, x⁰, x¹ ∈ Rⁿ be given.

BASIC PROBLEM OF THE CALCULUS OF VARIATIONS. Find a curve x^∗(.) : [0, T] → Rⁿ that minimizes the functional

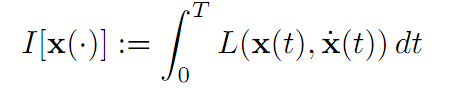(1.1)

among all functions x(.) satisfying x(0) = x0 and x(T) = x¹.

Now assume x^∗(.) solves our variational problem. The fundamental question is this: how can we characterize x^∗(.)?

1.1 DERIVATION OF EULER–LAGRANGE EQUATIONS.

NOTATION.We write L = L(x, v), and regard the variable x as denoting position,  the variable v as denoting velocity. The partial derivatives of L are

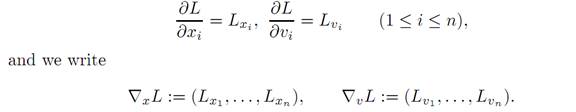
THEOREM 1.1 (EULER–LAGRANGE EQUATIONS). Let x^∗(.) solve the calculus of variations problem. Then x^∗(.) solves the Euler–Lagrange differential equations:

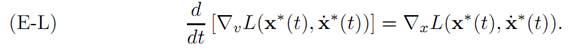
The significance of preceding theorem is that if we can solve the Euler–Lagrange equations (E-L), then the solution of our original calculus of variations problem  (assuming it exists) will be among the solutions.

Note that (E-L) is a quasilinear system of n second–order ODE. The i^th component of the system reads

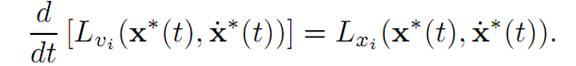
Proof. 1. Select any smooth curve y[0, T] → Rn, satisfying y(0) = y(T) = 0.

Define

i(τ ) := I[x(.) + τy(.)]

for τ ∈ R and x(.) = x^∗(.). (To simplify we omit the superscript ∗.) Notice that x(.) + τy(.) takes on the proper values at the endpoints. Hence, since x(.) is

minimizer, we have

                            i(τ ) ≥ I[x(.)] = i(0).

Consequently i(.) has a minimum at τ = 0, and so i′(0) = 0.

2. We must compute i′ (τ ). Note first that

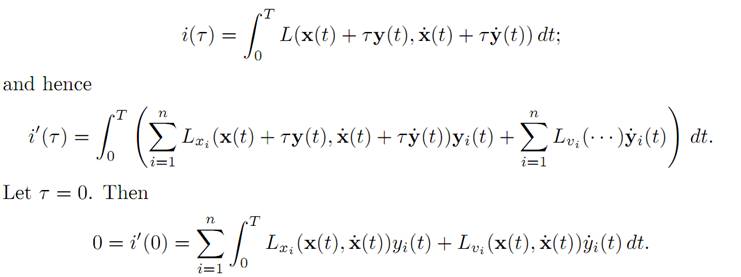
This equality holds for all choices of y : [0, T] → Rⁿ, with y(0) = y(T) = 0.

3. Fix any 1 ≤ j ≤ n. Choose y(.) so that

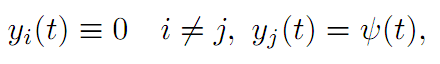
where ψ is an arbitary function. Use this choice of y(.) above:

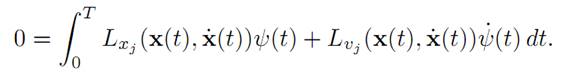
Integrate by parts, recalling that ψ(0) = ψ(T) = 0:

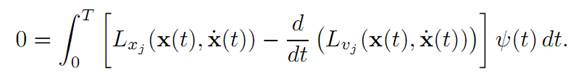
This holds for all ψ : [0, T] → R, ψ(0) = ψ(T) = 0 and therefore

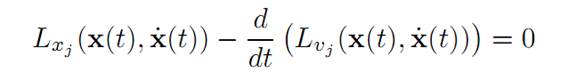
for all times 0 ≤ t ≤ T. To see this, observe that otherwise L_xj – d/dt (L_vj ) would be,  say, positive on some subinterval on I ⊆ [0, T]. Choose ψ ≡ 0 off I, ψ > 0 on I.

Then

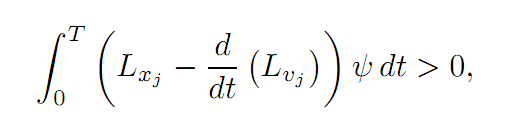
a contradiction.

1.2 CONVERSION TO HAMILTON’S EQUATIONS.

DEFINITION. For the given curve x(.), define

                                 p(t) := ∇_vL(x(t), x˙ (t))                            (0 ≤ t ≤ T).

We call p(.) the generalized momentum.

Our intention now is to rewrite the Euler–Lagrange equations as a system of first–order ODE for x(.), p(.).

IMPORTANT HYPOTHESIS: Assume that for all x, p ∈ Rⁿ, we can solve the equation

(1.2)                               p = ∇_vL(x, v)

for v in terms of x and p. That is, we suppose we can solve the identity (1.2) for

                                            v = v(x, p).

DEFINITION. Define the dynamical systems Hamiltonian H : Rⁿ × Rⁿ → R by the formula

                         H(x, p) = p . v(x, p) − L(x, v(x, p)),

where v is defined above.

NOTATION. The partial derivatives of H are

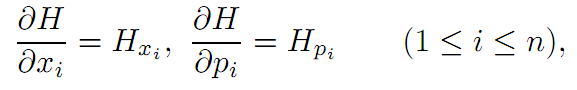
and we write

∇_xH := (H_x1 , . . . ,H_xn), ∇_pH := (H_p1 , . . . ,H_pn).

THEOREM 1.2 (HAMILTONIAN DYNAMICS). Let x(.) solve the EulerLagrange equations (E-L) and define p(.)as above. Then the pair (x(.), p(.)) solves Hamilton’s equations:

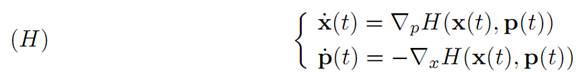
Furthermore, the mapping t → H(x(t), p(t)) is constant.

Proof. Recall that H(x, p) = p . v(x, p) − L(x, v(x, p)), where v = v(x, p) or,  equivalently, p = ∇_vL(x, v). Then

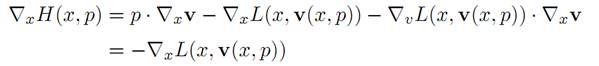
because p = ∇_vL. Now p(t) = ∇_vL(x(t), x˙ (t)) if and only if x˙ (t) = v(x(t), p(t)).

Therefore (E-L) implies

A PHYSICAL EXAMPLE. We define the Lagrangian

which we interpret as the kinetic energy minus the potential energy V . Then

∇_xL = −∇V (x), ∇_vL = mv.

Therefore the Euler-Lagrange equation is

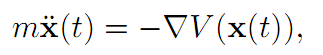
which is Newton’s law. Furthermore

                       p = ∇_vL(x, v) = mv

is the momentum, and the Hamiltonian is

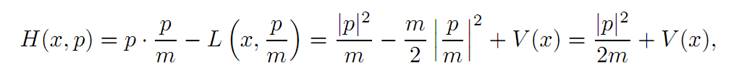
the sum of the kinetic and potential energies. For this example, Hamilton’s equations read

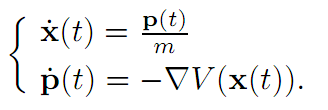
References

[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.

[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.

[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.

[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.

[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.

[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.

[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.

[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.

[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.

[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).

[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.

[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.

[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.

[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.

[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.

[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.

[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.

[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.

[T] William J. Terrell, Some fundamental control theory I: Controllability, observability,  and duality, American Math Monthly 106 (1999), 705–719.