Shallow Square Well I

A particle of mass m moving in one dimension has a potential V(x) which is a shallow square well near the origin:

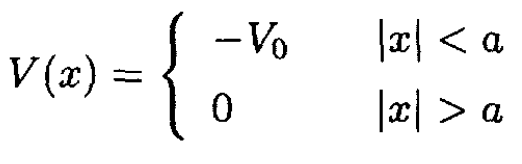(1)

where V₀ is a positive constant. Derive the eigenvalue equation for the state of lowest energy, which is a bound state (see Figure 1.1).

Figure 1.1

SOLUTION

The ground state energy E must be less than zero and greater than the bottom of the well, 0 > E > -V₀. From the expression

(1)

one can deduce the form for the eigenfunction. Denote the ground state energy E = -h²α²/2m, where α is to be determined. The eigenfunction outside the well (V = 0) has the form exp(-α|x|). Inside the well, define k² = k²₀ – α², where k²₀ = 2mV₀/h². One can show that k² is positive since E + V₀ > 0. Inside the well, the eigenfunction has the form A cos kx, so

(2)

Matching ѱ(x) and its derivative at x = a gives two expressions:

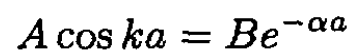(3)

(4)

Dividing these two equations produces the eigenvalue equation

(5)

The equation given by the rightmost equals sign is an equation for the unknown k. Solving it gives the eigenvalue E.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يوزع أكثر من ألفي وجبة طعام للمعزين في ذكرى عاشوراء بنينوى

قسم الشؤون الطبية يواصل تقديم خدماته الصحية لزائري عاشوراء

جموع المعزين تحيي مراسم يوم العاشر من شهر المحرم عند المرقدين الطاهرين

قسم العلاقات يطلق محطات فتية الكفيل الثقافية في محافظة نينوى

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين