Dielectric Cylinder in Uniform Electric Field

An infinitely long circular cylinder of radius a, dielectric constant ε, is placed with its axis along the z-axis, and in an electric field which would be uniform in the absence of the cylinder, E = E₀ x (see Figure 1.1). Find

Figure 1.1

the electric field at points outside and inside the cylinder and the bound surface charge density.

SOLUTION

First solution: Introduce polar coordinates in the plane perpendicular to the axis of the cylinder (see Figure 1.2). In the same manner as,

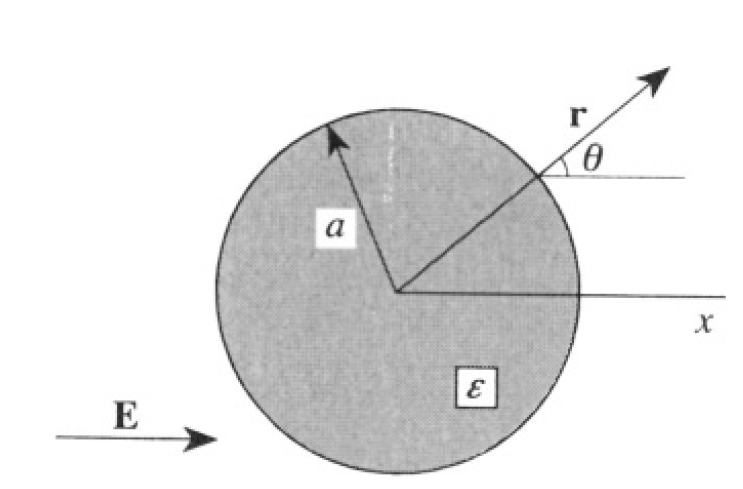
Figure 1.2

we will look for a potential outside the cylinder of the form

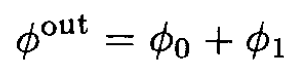(1)

where ϕ₀ = -E . r and ϕ₁ is a solution of the two-dimensional Laplace equation, which may depend on one constant vector E

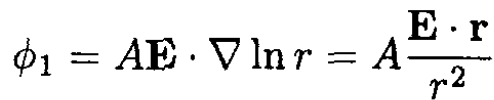(2)

where A is some constant. Inside the cylinder, the only solution of Laplace’s equation that is bounded in the center of the cylinder and depends on E is

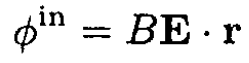
Using the condition on the potential ϕ at r = a, ϕⁱⁿ = ϕ^out we find

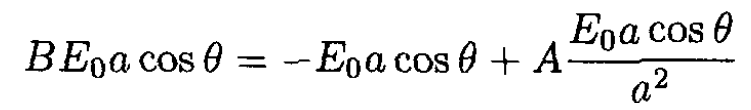(3)

from which we find

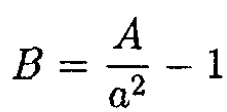
We now have

(4)

(5)

Using the boundary condition Dⁱⁿ_n = D^out_n or Eⁱⁿ_n = εE^out_n, we find

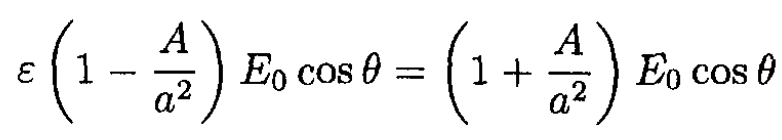
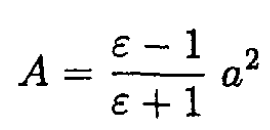
So we obtain

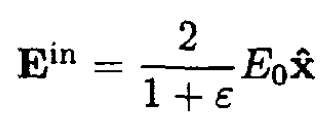(6)

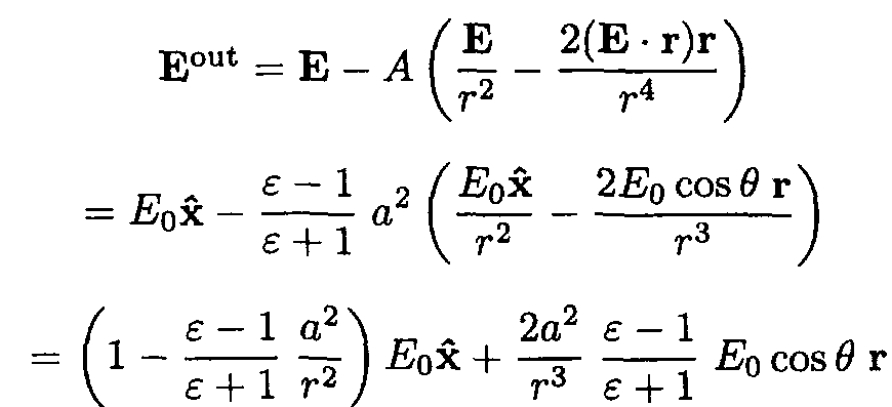(7)

The polarization is

So the dipole moment per unit length of the cylinder is

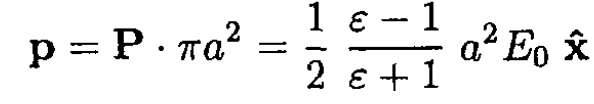
which corresponds to the potential

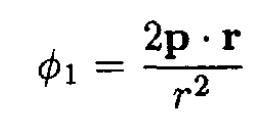
The surface charge density σ is

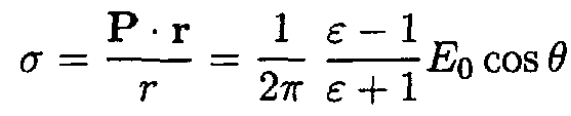
Second solution: Use the fact that for any dielectric ellipsoid with a dielectric constant ε immersed in a uniform electric field in vacuum, a uniform electric field inside is created. Therefore there must be a linear dependence between E_0x, Eⁱⁿ_x, and Dⁱⁿ_x, where the applied field E₀ is along the x-axis

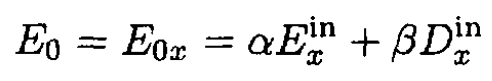(8)

where α and β are coefficients independent of the dielectric constant of the ellipsoid and only depend on its shape. For the trivial case in which ε = 1

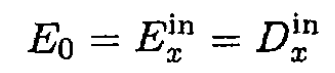
Therefore

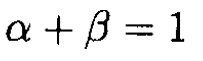(9)

For a conducting ellipsoid (which can be described by a dielectric constant ε = ∞)

where n_x is the depolarization factor. From (9), we have

Finally (8) takes the form

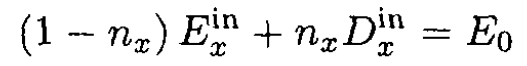(10)

For a cylinder parallel to the applied field along the z-axis, n_z = 0, but n_x + n_y +n_z = 1, so n_x = n_y = 1/2. Equation (10) becomes

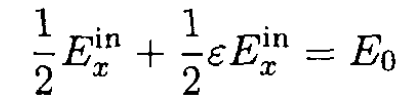(11)

and

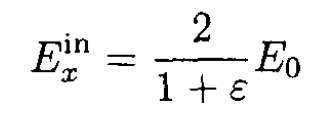(12)

as in (6) above.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين