
Collapsed Star
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 78
الجزء والصفحة:
part 2 , p 78
 14-8-2016
14-8-2016
 1384
1384
Collapsed Star
In a very simple model of a collapsed star a large number A = N + Z of nucleons (N neutrons and Z protons) and Z electrons (to ensure electric neutrality) are placed in a one-dimensional box (i.e., an infinite square well) of length L. The neutron and proton have equal mass 1 GeV, and the electron has mass 0.5 M eV Assume the nucleon number density is λ = 0.5 fm-1 (1 fm = 10-13 cm), neglect all interactions between the particles in the well, and approximate Z >> 1.
a) Which particle species are relativistic?
b) Calculate the ground state energy of the system as a function of Z for all possible configurations Z/A with fixed A.
c) What value of Z/A (assumed small) minimizes the total energy of the system?
SOLUTION
a) Using the 1D Schrodinger equation
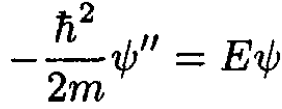 (1)
(1)
with the boundary conditions ѱ(L/2) = ѱ(-L/2) = 0 gives
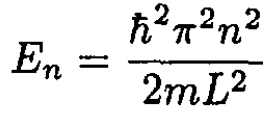 (2)
(2)
where n = 1, 2, 3,… . Protons, neutrons, and electrons are spin-1/2 fermions, so 2 may occupy each energy level, and we have
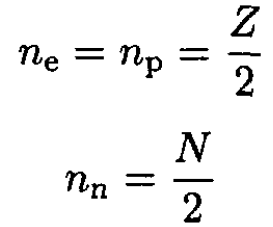
The kinetic energy of a particle
 (3)
(3)
where
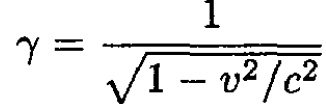 (4)
(4)
To determine which species are relativistic, we wish to find whether γ >> 1. We may extract γ from (2). For neutrons:
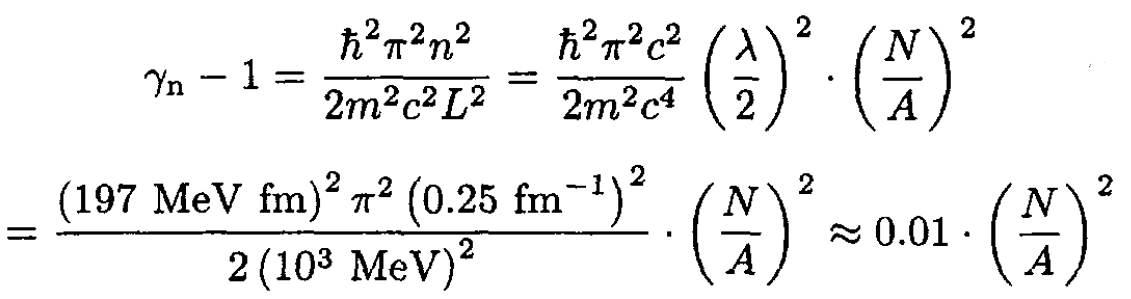 (5)
(5)
Similarly for protons:
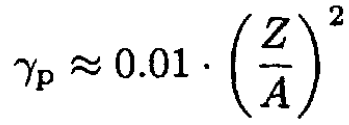 (6)
(6)
Since N, Z < A, both neutrons and protons are non-relativistic. For electrons:
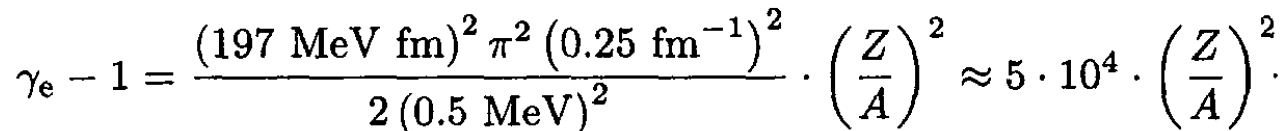 (7)
(7)
The equilibrium value of Z/A obtained in (c) for relativistic electrons gives Z/A ~ 0.07 which still leaves γe >> 1 in (7). Moreover, if we assume that the electrons are non-relativistic and minimize (14) below with electron energy (see 9)
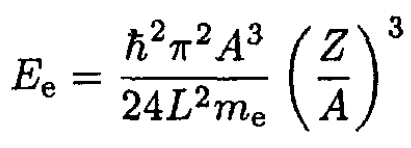 (8)
(8)
we will get Z/A ~ 0.02 and γe ≈ 20 which contradicts the assumption. So the electrons are relativistic. Alternatively
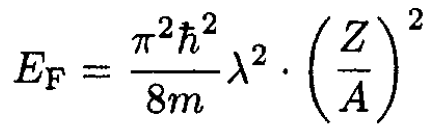
the same as (5).
b) The ground state energy of the system is given by the sum of energies of all levels, which we may approximate by an integral. We calculate the total energies of non-relativistic particles (neutrons and protons) and relativistic ones (electrons) separately:
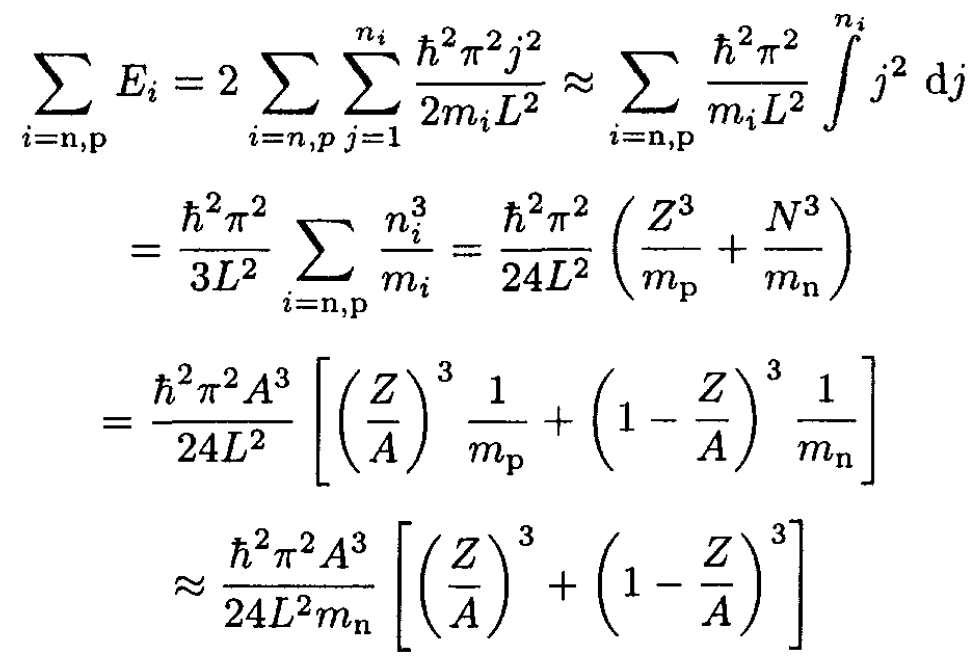 (9)
(9)
For 1-D electrons
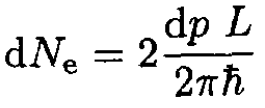 (10)
(10)
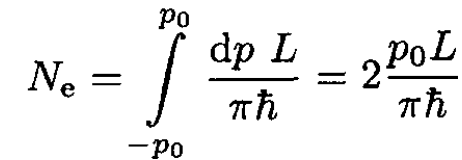 (11)
(11)
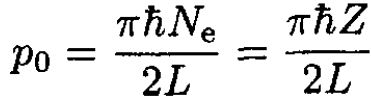 (12)
(12)
The total electron energy is
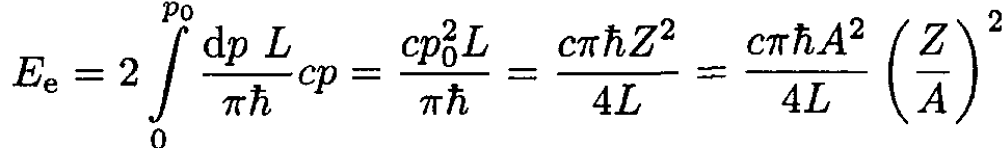 (13)
(13)
where we used for an estimate an electron energy of the form E = cp since we have already established that they are relativistic. We can obtain a correct value of γe for them:
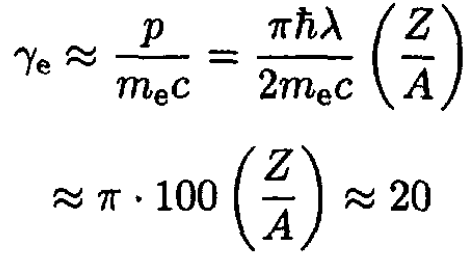
where we have used the result of (c), Z/A ≈ 0.07. The total energy of the star is
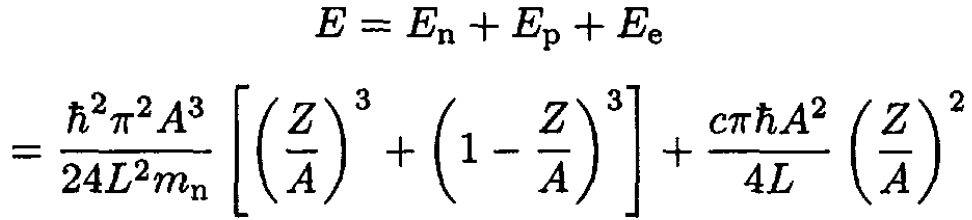 (14)
(14)
c) Let x ≡ Z/A. We need to find the minimum of the expression
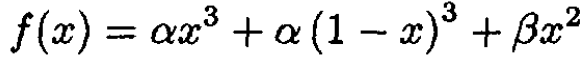 (15)
(15)
where
 (16)
(16)
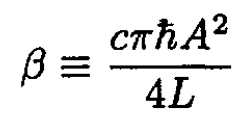 (17)
(17)
Setting the derivative of (15) equal to zero gives
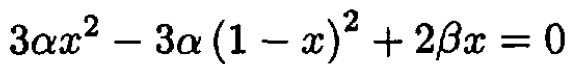 (18)
(18)
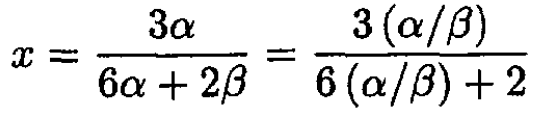 (19)
(19)
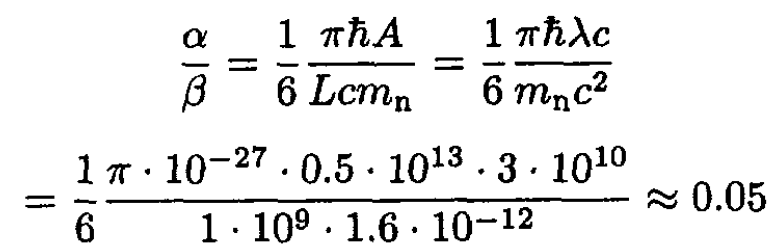 (20)
(20)
Finally,
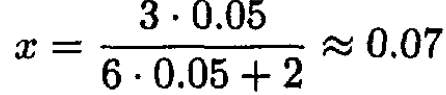 (21)
(21)
So the minimum energy corresponds to a star consisting mostly (~93%) of neutrons.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


