Potential of Halved Cylinder

Consider an infinitely long conducting cylinder of radius a with its axis coinciding with the z-axis. One half of the cylinder (cut the long way) (y > 0) is kept at a constant potential V₀, while the other half (y < 0) is

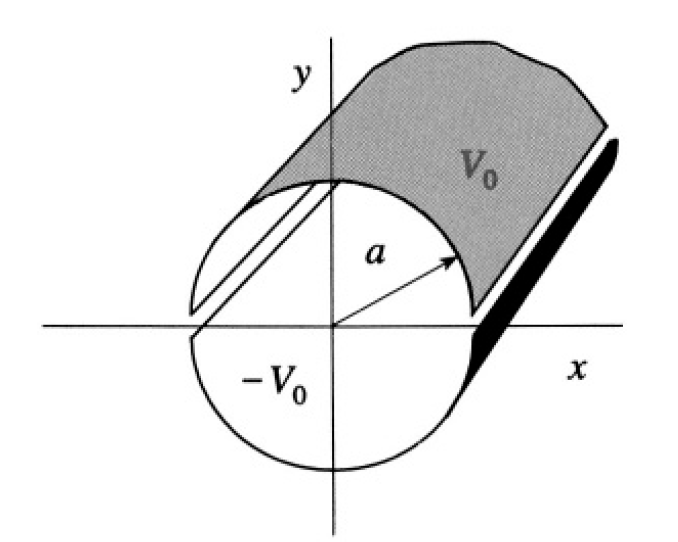
Figure 1.1

kept at a constant potential –V₀ (see Figure 1.1). Find the potential for all points inside the cylinder and the field E along the z-axis.

SOLUTION

This problem can be solved by several methods. We will use conformal mapping. Namely, we will try to find a function ω (z), where z = x + iy, to transform the curves of equal potential (in the cross section of the three dimensional body) into parallel straight lines in the u – v plane, where ω = u + iv = f (x, y) +ig (x, y) with both f and g satisfying the Laplace’s equation. We can easily find the solution for the potential problem in the ω plane, and because of the properties of a conformal mapping, the functions u = f (x, y) or v = g (x, y) will be a solution to the initial potential problem. For this problem, we can use the transformation

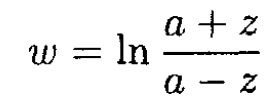(1)

This will transform a circle R = a into two straight lines (see Figure 1.2). The upper half of the cylinder will go into v = π/2, and the lower half will

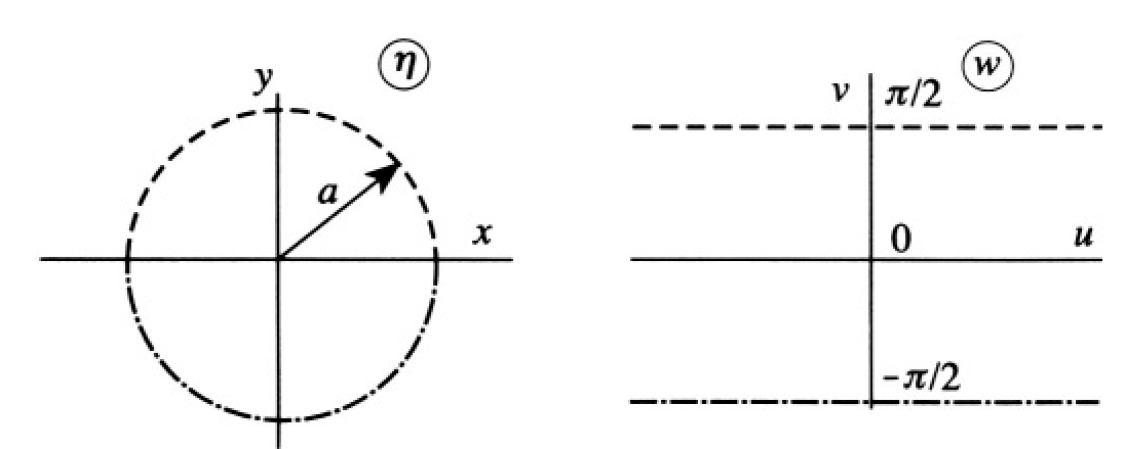
Figure 1.2

go into v = -π/2. So we have

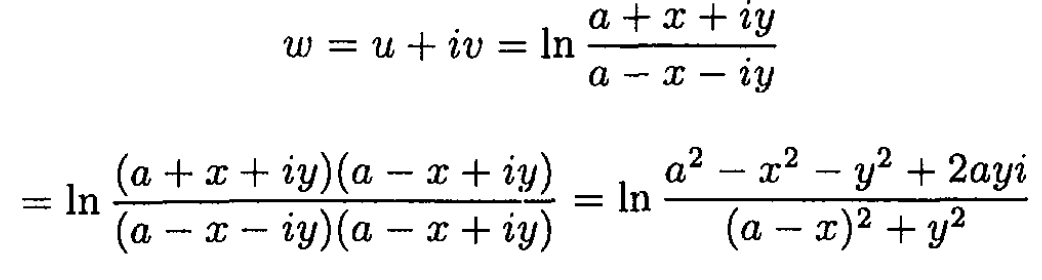(2)

Denote the argument of the natural log as ρe^iφ where ρ and φ are real. Then.

So v = φ. On the other hand,

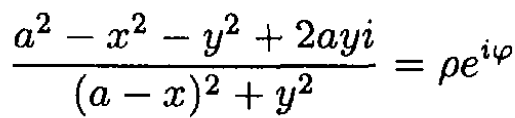(3)

For a complex number m + in = ρe^iφ, we have

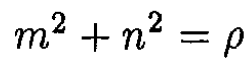(4)

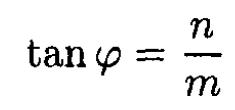(5)

Using (5), we obtain from (3)

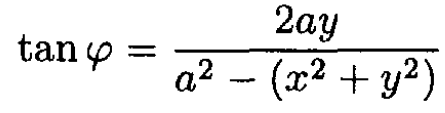
or

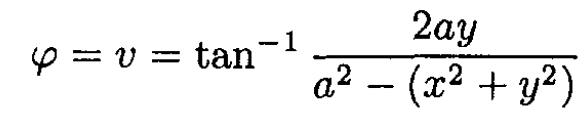
So the potential which satisfies ϕ(v = -π/2) = -V₀, ϕ(v = π/2) = V₀ is

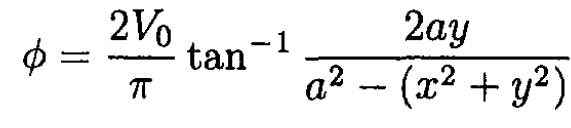(6)

On the z-axis

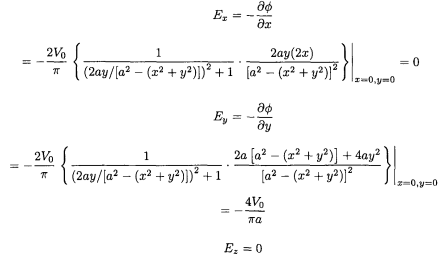
A different solution to this problem may be found in Cronin, Greenberg.