


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 25-7-2016
Date: 4-9-2016
Date: 19-8-2016
|
Lifetime of Classical Atom
At a time t = 0, the electron orbits a classical hydrogen atom at a radius a0 equal to the first Bohr radius. Derive an expression for the time it takes for the radius to decrease to zero due to radiation. Assume that the energy loss per revolution is small compared to the total energy of the atom.
SOLUTION
If the energy loss per revolution is small compared to the total energy of the electron in the atom, we can write
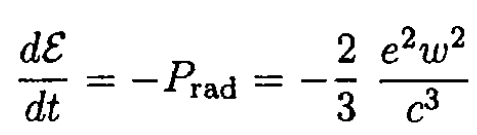 (1)
(1)
where ω is the acceleration of the electron and Prad is the total radiated power. Using our assumption, we can approximate the orbit of the electron (which is a spiral) by a circle for each revolution of radius r = r(t). The acceleration is due to the Coulomb force
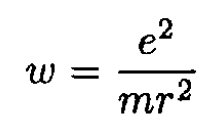 (2)
(2)
On the other hand, using |ε| = |U|/2 (U is the potential energy of a particle moving in a circle in a 1/r2 field) we have
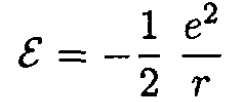 (3)
(3)
Substituting (2) and (3) into (1) gives
 (4)
(4)
or
 (5)
(5)
Integrating (5) yields
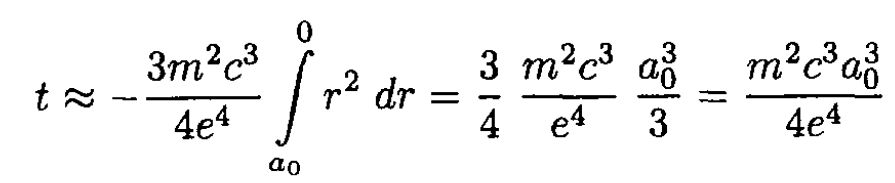
So
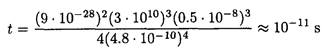



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|