


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-8-2016
Date: 23-8-2016
Date: 29-8-2016
|
Bug on Globe
A toy globe rotates freely without friction with an initial angular velocity ω0. A bug starting at one pole N travels to the other pole S along a meridian with constant velocity v. The axis of rotation of the globe is held fixed. Let M and R denote the mass and radius of the globe (a solid sphere, moment of inertia I0 = 2MR2/5, m the mass of the bug, and T the duration of the bug's journey (see Figure 1.1).
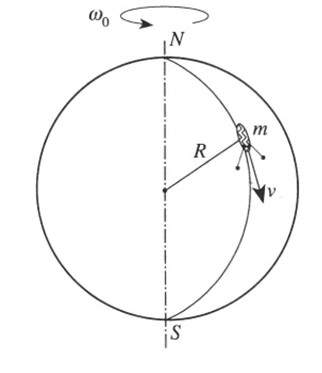
Figure 1.1
Show that, during the time the bug is traveling, the globe rotates through an angle
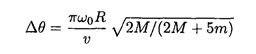
A useful integral is
SOLUTION
The angular velocity of the globe is always in the same direction (along the fixed axis, see Figure 1.2). Since the angular momentum 1 is constant
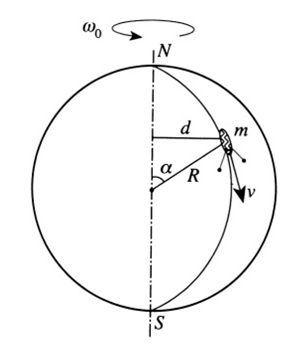
Figure 1.2
And |1| = Iω we may write
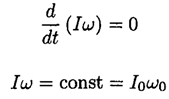 (1)
(1)
Initially I0 is just the moment of inertia of the sphere (the bug is at the pole), so I0 = (2/5)MR2. Substituting this into (1) we obtain

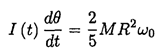
where 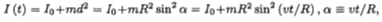 so
so


We used here sin2 (x/2) = (1/2)(1-cos x) and the integral given in the problem:
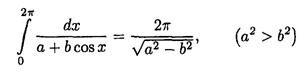

If the bug had mass m = 0, the angle ∆θ would be

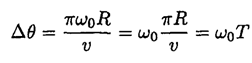
which corresponds to the free rotation of the globe with angular velocityω0.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
خدمات متعددة يقدمها قسم الشؤون الخدمية للزائرين
|
|
|