


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 1-8-2016
Date: 30-8-2016
Date: 7-8-2016
|
Cue-Struck Billiard Ball
Consider a homogeneous billiard ball of mass m and radius R that moves on a horizontal table. Gravity acts downward. The coefficient of kinetic friction between the ball and the table is μ, and you are to assume that there is no work done by friction for pure rolling motion. At time t = 0 the ball is struck with a cue, which delivers a force pulse of short duration. Its impulse is
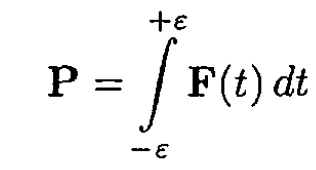
a) The point of contact between the cue and the ball is at the “equator” and the direction of the force is toward the center of the ball. Calculate the time at which pure rolling motion begins. What is the final speed of the center of mass of the ball?
b) At what height h above the center must the cue strike the ball so that rolling motion starts immediately (see Figure1.1)?

Figure1.1
SOLUTION
a) Introduce a frame of reference with the origin at the center of the ball (see Figure 1.2a). Since the direction of the force is toward the center of the ball there is no torque at t = 0. (We consider a very short pulse.) So one can define the initial conditions of the ball’s movement from the
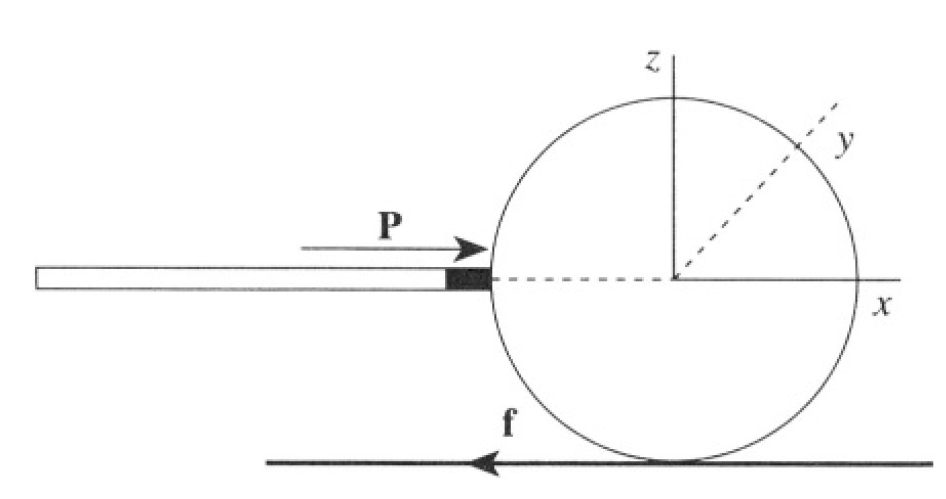
Figure 1.2a
equations
 (1)
(1)
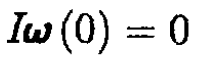
where v(0) and ω(0) are the velocity and angular velocity at t = 0 and I is the moment of inertia of the ball I = (2/5) mR2. So we have v(0) = P/m and ω(0) = 0. Subsequent motion of the ball will be given by
 (2)
(2)
where f is a friction force 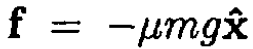 and ω = ωŷ. In our geometry, (2) may be rewritten in the form
and ω = ωŷ. In our geometry, (2) may be rewritten in the form
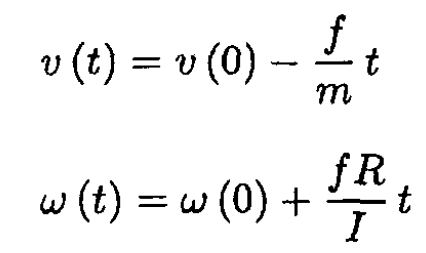 (3)
(3)
The ball will roll without slipping when v = ω × R or v = ωR. Using
(3), we obtain the time tR when pure rolling motion begins:
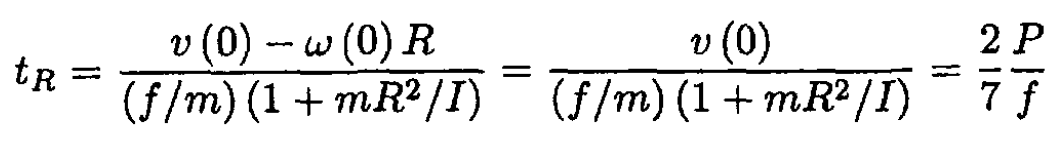
The final speed vf of the center of mass of the ball is given by

b) Using (1) from part (a) for the initial conditions, we obtain
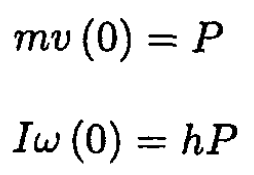

Figure 1.2b
Again using the condition v(0) = ω(0) R for rolling without slipping, we have (see Figure 1.2b)
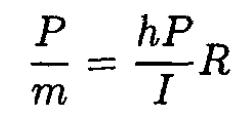
and
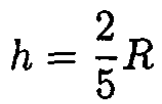



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|