A block of a graph G is a maximal induced connected subgraph without a cut vertex (of itself as a graph).We verify the following properties of blocks (do these verifications as exercises):

               – the blocks define a partition of the set of the edges of G;

             – two blocks may share at the most only one vertex of G, that vertex is then a cut vertex of G. Conversely, a cut vertex of G is a vertex shared  by at least two blocks of G.

The set of blocks of G constitutes the block decomposition of G. It is unique and it is a finer decomposition of the graph than the one defined by the connected components. Many properties or graph processings can be brought back to these blocks. There are some good algorithms (with linear complexity) which determine the blocks of a graph.

Figure 1.1 gives an example of block decomposition of a graph.

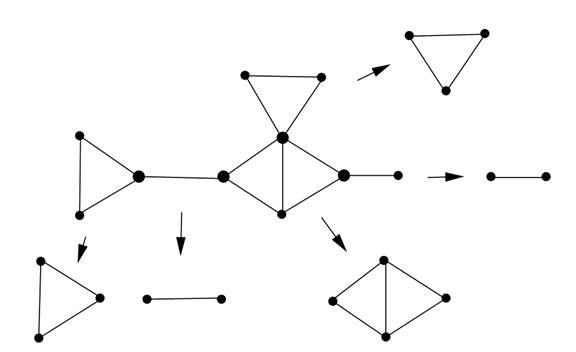
Figure 1.1. A graph and its blocks (the cutvertices of the graph are in bold)

____________________________________________________________________________________

Graph Theory  and Applications ,Jean-Claude Fournier, WILEY, page(60)