


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 10-3-2021
Date: 29-11-2020
Date: 15-12-2016
|
Force, Mass and Acceleration
In the previous section it was recognized that to move a trolley from rest required the application of a force. To move a car from rest would require a much greater force-a car has much greater resistance to motion or inertia. A measure of this inertia is what is called the mass of the trolley or car. Mass is intimately related to weight but is fundamentally different. The weight of an object is the gravitational force exerted on it by the earth and is measured, for example, by weighing it using a spring balance. An object weighed on the moon will have one-sixth of its weight on the earth simply because the moon is smaller and less massive than the earth and therefore exerts less gravitational attraction. Mass, on the other hand, is intrinsic to the body and has the same value wherever the body is; it is essentially just as hard to move a car from rest on the moon as it is on the earth! The effect of exerting a force on a body is to make it move faster in the direction of the force; the body accelerates. If this is the only force acting on the body then the acceleration will be steady and the body will move faster and faster. The size of this acceleration is proportional to the size of the force and, as should be expected from our discussion of the trolley and the car, will be smaller the more massive the body. In fact the relationship between force, mass and acceleration is very simple

This relationship is enshrined in Newton’s Second Law of Motion.
Newton’s Second Law of Motion. The acceleration of a body is proportional to the force applied and is in the direction of that force.
In the above equation we see that the constant of proportionality is the inverse of the mass of the body. Of course, if a body is already in steady motion and a force is applied in a direction opposite to that motion then deceleration proportional to the force takes place. The strength of a force is measured in what are called newtons (denoted by N) where one newton (1N) is the force needed to give one kilogram (1 kg) an acceleration of one metre per second per second (1 m s-2).
Newton also formulated a Third Law.
Newton’s Third Law of Motion. When two bodies interact with each other the force on the first body due to the second is equal and opposite to the force on the second body due to the first.
For example, a weight placed on a table exerts a downward force on the table due to the pull of gravity. In turn the table exerts an equal upward force on the weight (see figure 1.1). If this (reaction) force were bigger there would be a net upward force
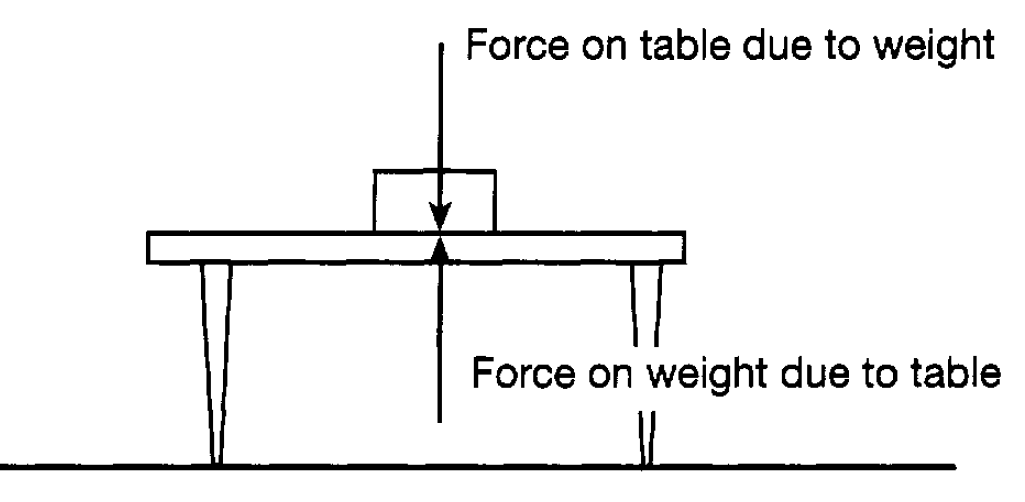
Figure 1.1: Equal and opposite forces acting on a weight and a table.
and the weight would move upwards; similarly if less than the downward force the weight would move downwards. Obviously neither of these situations can occur! It is interesting at this stage to say a little more about the force of gravity. This force is proportional to the product of the masses of the two bodies interacting. In mathematical terms, if the masses of the two bodies (measured in kilograms) are m and M and their distance apart (measured in metres) is r, then the magnitude of the force F (measured in newtons) which each experiences pulling it towards the other is given by

where G is known as the gravitational constant and has the value G = 6.67 ×10-11 N m2 kg-l. It is a measure of the strength of the gravitational interaction Here it is important to note that we have been discussing ''mass'' in two different ways. As first introduced it is that quantity which specifies the inertia of a body and which determines the degree to which the body accelerates when a force is applied. In this context it is referred to as the inertial mass. Its second use has been as the quantity which determines the size of the gravitational force a body experiences due to another body as given in the above formula. In this second context it is referred to as the gravitational mass. The important point to note is that we find that these two different masses are identical. The above law of gravitational attraction means that, on the earth, the gravitational forces experienced by different bodies are simply proportional to their mass since the mass of the earth is obviously common to all situations. Since the acceleration produced by this force is inversely proportional to the mass it follows that the acceleration down to the earth of a body dropped from a height is the same whatever its mass; the more massive the body the stronger the force of gravity, but the harder it is to accelerate it. This is not quite observed in practice since there is friction from the air (air resistance) and so in reality the net force on a falling body is gravity less air resistance and the latter will be different for differently shaped bodies and for different speeds of fall. However, if the bodies are reasonably heavy so that air resistance is negligible compared with the gravitational force then they will fall with very nearly the same acceleration. This was established first by Galileo in the 16th century when he is believed to have demonstrated this by dropping objects from the leaning tower of Pisa. On the moon, where there is no atmosphere, a lead weight and a feather will fall at the same speed. It is interesting to note that if the falling object on the earth is, for example, a person wearing a parachute, then the air resistance increases significantly as the speed of fall increases until, quite soon, it is equal to the force of gravity but is, of course, in the opposite direction. There is then zero net force and therefore zero acceleration so the falling person no longer accelerates and travels down to the earth at a constant and reasonably safe speed. Without a parachute the air resistance is much less and only balances the gravitational force at a much higher speed.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|