Enzyme Kinetic Mechanisms

The term kinetic mechanism used with enzymes refers to the order of substrate addition to, and product release from, the enzyme. The procedure that is now used widely for describing kinetic mechanisms was introduced by W. W. Cleland in 1963 (1). It involves the use of the letters A, B, and C for substrates; P, Q, and R for products; E and F for stable enzyme forms. For illustrative purposes, the enzyme is represented by a horizontal line, and the enzyme-reactant complexes are shown below the line. The reversible addition of substrates, and release of products, are denoted by single, vertical arrows. When required, rate constants for the forward and reverse steps of each reaction are written to the left and right of the vertical arrows, respectively.

 The types of kinetic mechanisms that apply, and the shorthand procedure for describing them, can be well illustrated by reference to reactions involving two substrates and two products. These Bi–Bi reactions form a high proportion of all known enzymic reactions and include those catalyzed by dehydrogenases and phosphotransferases (see Kinase). The mechanisms fall into two broad categories: sequential and nonsequential (Fig. 1). 

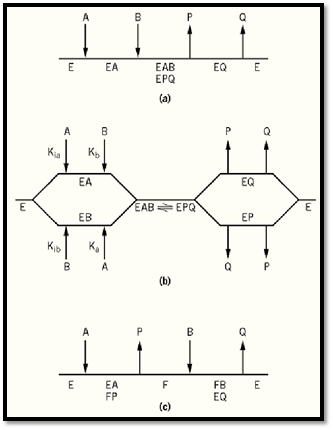
Figure 1. Kinetic mechanisms for reactions involving two substrates (A and B) and two products (P and Q). (a( Ordered. (b) Random. (c) Ping-pong.

1. Sequential Mechanisms

Sequential mechanisms are characterized by the fact that both substrates must add to the enzyme before either product is released. This category has two basic subdivisions: ordered and random.

1.1. Ordered Mechanisms 

In an ordered mechanism, there is a compulsory order of substrate addition and product release (Fig. 1a). The native enzyme possesses a binding site for substrate A, and formation of the EA complex results in the creation of a binding site for substrate B. This is most likely due to the binary enzyme–substrate complex undergoing a conformational change  or the highly synergistic binding of the two substrates, in which case the tightly bound one appears to bind first (2). After formation of the ternary EAB complex, the chemical reactions occur, with the formation of an EPQ complex. These two ternary, or central, complexes are treated as a single entity because steady-state kinetic studies, except for isotope effects, do not permit the detection of unimolecular isomerizations and cannot distinguish between them. Further, the inclusion of such isomerization steps does not affect the form of the steady-state rate equations. The mechanism is usually symmetrical, with the product of the first substrate to add being the last to dissociate from the enzyme. Many dehydrogenases conform to this mechanism, with NAD or NADP being the first substrate to add, and NADH or NADPH the last product to be released (3). When no assumptions are made about the relative rates of the various reaction steps, the mechanism is referred to as steady-state-ordered. The Theorell–Chance mechanism is a special case of an ordered mechanism where the steady-state concentrations of the ternary complexes, such as E-NAD-ethanol and E-NADPH-acetaldehyde, are kinetically insignificant (4). However, this is just a matter of degree, and the formation of these ternary complexes can be demonstrated by means of product inhibition studies, or better still by isotope exchange at equilibrium.

Another special case in the ordered category is the equilibrium ordered mechanism, where the interaction between E and A occurs at thermodynamic equilibrium. This mechanism is observed when a metal ion is an essential activator and must interact to form an active enzyme with which the substrate then reacts (5). It can also occur when the off rate constant is considerably greater than the turnover number .

1.2. Random Mechanisms 

Enzymes conforming to a random kinetic mechanism possess distinct binding sites for each of the two substrate–product pairs. Thus, either substrate can add to the enzyme either before or after the other substrate (Fig. 1b). The same principle applies to product release. The presence of one substrate on the enzyme can enhance, hinder, or have no effect on the binding of the other. It is also possible for one substrate, and the product of the other substrate, to be present on the enzyme at the same time. The formation of such a dead-end complex will always occur with the smaller substrate–product pair, but not necessarily with the larger substrate–product pair if there is sufficient steric hindrance. Several phosphotransferases (kinases) exhibit random kinetic mechanisms (6, 7).

2. Nonsequential Mechanisms

2.1.  Ping-Pong Mechanisms 

The representative of the nonsequential mechanisms is the single-site ping-pong mechanism (Fig. 1c). The first substrate to bind possesses a donor group that is transferred to the native enzyme E, to form a new stable form of enzyme F and the product P is released. The second substrate B reacts at the site that P has vacated, and the donor group on the enzyme is transferred to B to form Q. Aminotransferases have this mechanism, with the amino group of an amino acid being transferred to the cofactor pyridoxal phosphate, to form a pyridoxamine-phosphate enzyme and subsequently to an a-keto acid (8). Nucleoside diphosphokinase also has a pong-pong mechanism, with F being a phosphorylated enzyme (9). The F form of enzyme can be isolated and used for stoichiometric reaction with B. A characteristic feature of enzymes conforming to a ping-pong reaction mechanism is that they catalyze partial exchange reactions  and have substrates of a similar structure. There are also enzymes, such as transcarboxylase (10), that catalyze two-site ping-pong mechanisms, and several that exhibit multisite ping-pong mechanisms (11). In these cases, an enzyme-bound carrier such as biotin, lipoic acid, or 4-phosphopantetheine serves to carry the transferred moiety between the separate sites.

 3. Initial Rate Equations for Sequential Mechanisms

3.1. Steady-State-Ordered and Rapid-Equilibrium Random Mechanisms 

Under conditions where catalysis is not solely rate-limiting, initial velocity data for a random mechanism would yield nonlinear double-reciprocal plots (see Lineweaver–Burk Plot). But such nonlinearity cannot generally be detected with steady-state kinetic techniques, and random mechanisms behave as though they are of the rapid-equilibrium random type, with the interconversions of the ternary EAB and EPQ complexes being the slow steps of the reaction sequence in each direction. The initial velocity equation for rapid-equilibrium random and steady-state-ordered mechanisms has the same form (Eq. (1)):

where V is the maximum velocity of the reaction; K_a and K_b are the K_m (Michaelis constants) for the substrates A and B, respectively; A and B are their respective concentrations; and K_ia is the dissociation constant for the complex EA. The numerator of Equation (1) represents the driving force of the reaction, and the denominator represents the distribution of the enzyme among its various forms. For the rapid-equilibrium random reaction, the four terms of the denominator denote the proportion of total enzyme that is present as free enzyme, EB, EA, and EAB, respectively. Because catalysis is slow relative to product release, no significant concentrations of EP and EQ will be present (Fig. 1b).

 For a steady-state ordered mechanism, the K_iaK_b and K_aB terms represent the free enzyme, K_bA the EA complex, and AB the combined concentrations of the EAB, EPQ, and EQ complexes (Fig. 1a). The reciprocal form of Equation (1), with A as the variable substrate, is given in Equation (2):

 This equation indicates that a double-reciprocal plot of 1/v against 1/A at different fixed concentrations of B would yield a family of straight lines that intersect to the left of the vertical ordinate, with the slopes and intercepts of the lines varying as a function of the concentration of B ) Fig. 2). This is known as a primary plot. Equation (1) is symmetrical, so the double-reciprocal plot with B as the variable substrate will have the same general form as Equation (2). The coordinates of the crossover point would be –1/K_ia and (1/V) [1–K_a/K_ia] with A as the variable substrate and –K_a/ (K_iaK_b) and (1/V) [ 1–K_a/K_ia] with B as the variable substrate.

Figure 2. Intersecting initial velocity pattern for a steady-state-ordered or rapid-equilibrium random mechanism obtained upon varying substrate A, at different fixed concentrations of substrate B. A similar pattern would be observed with B as the variable substrate. Values chosen for the kinetic parameters were V, 0.2; K_ia, 0.33; K_a, 0.05; K_b, 4.0, in arbitrary units.

For a rapid-equilibrium random mechanism, K_a/(K_iaK_b) would be equal to K/K_ib, as for this mechanism K_iaK_b = K_aK_ib (Fig. 1b). It should be noted that the value of K_a/K_ia determines whether the lines cross above, on, or below the abscissa and the position of the crossover point, in relation to the abscissa, is independent of which substrate is varied. The initial velocity patterns for the steady-state-ordered and rapid-equilibrium random mechanisms are of the symmetrical intersecting type. From replots of the slopes and intercepts of the primary plots as a function of the reciprocals of the concentrations of the changing fixed substrate concentration, it is possible to determine values for each of the kinetic parameters. However, it is preferable to obtain these values by performing an overall fit of the initial velocity data to Equation (1) (12). Initial velocity patterns do not allow a distinction to be made between a steady-state-ordered and rapid-equilibrium random mechanism. Further, if the mechanism is of the steady-state-ordered type, it is not possible to assign the K_ia value to a particular substrate.

3.2 Equilibrium Ordered Mechanism 

An equilibrium ordered-mechanism is described by Equation (3): 

It differs from Equation (1) in not having a denominator term in B. That is, the value for K_a is essentially zero, and the free form of enzyme is represented by the single term, K_iaK_b. In contrast to Equation (1), Equation (3) is asymmetric. Rearrangement of this equation in double-reciprocal form yields Equations (4) and (5), with A and B as the variable substrates: 

These equations indicate that although the initial velocity patterns are of the intersecting type, they are not symmetrical. The pattern with A as the variable substrate intersects to the left of the vertical ordinate, with coordinates of the crossover point being –1/K_ia and 1/V. With B as the variable substrate, the lines intersect on the vertical ordinate (Fig. 3). The crossover point for this mechanism, with either A or B as the variable substrate, must lie above the abscissa. Further, a replot of the slopes of the primary plot with A as the variable substrate vs 1/B yields a straight line that passes through the origin. A replot of the intercepts of the primary plot with A as the variable substrate vs 1/B would give values for V and K_b (Eq. (4)), and a replot of the slopes of the primary plot with B as the variable substrate vs 1/A would yield a value for K_ia.

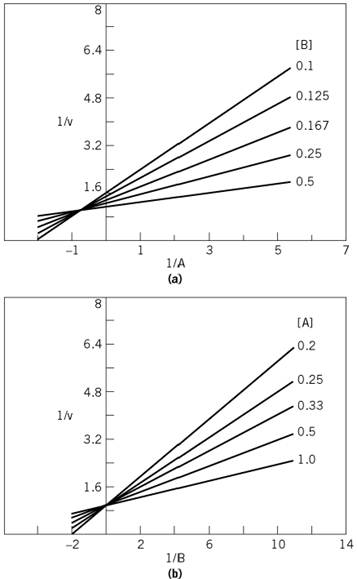
Figure 3. Asymmetric intersecting initial velocity patterns for an equilibrium-ordered mechanism. (a) Varying substrate A, at different fixed concentrations of substrate B. (b) Varying substrate B, at different fixed concentrations of substrate A. The patterns were produced by using values in arbitrary units for V, K_ia, and K_b of 1.0, 1.35, and 0.06, respectively.

3.3. Ping-Pong Mechanism 

A reaction conforming to a single-site ping-pong mechanism is described by Equation (6): 

This is a symmetrical equation, without a constant term in the denominator, which contains only the Michaelis constants for the two substrates. K_aB and K_bA represent the E and F forms of enzyme, respectively, and AB represents all the binary enzyme-reactant complexes. Rearrangement of Equation (6) in double-reciprocal form with A and B as variable substrates gives Equations (7) and (8), respectively: 

These equations indicate that the slopes of the lines do not vary with the concentration of the changing fixed substrate (B or A), and thus, the initial velocity patterns consist of families of parallel straight lines (Fig. 4) The patterns are symmetrical. Values for V, K_a, and K_b can be obtained from replots of the intercepts as a function of the reciprocals of the concentrations of the changing fixed substrate. 

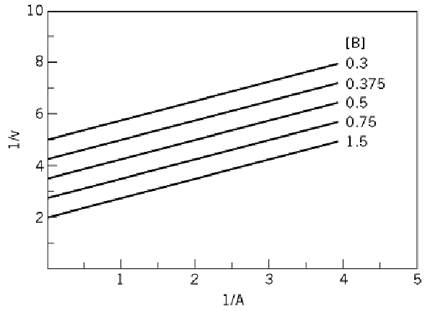
Figure 4. Parallel initial velocity pattern for a ping-pong mechanism as obtained by varying substrate A at different fixed concentrations of substrate B. The values in arbitrary units for V, K_a, and K_b were 0.8, 0.6, and 0.9, respectively.

Some caution must be exercised when an initial velocity pattern seems to consist of parallel straight lines. It may be that the lines intersect below the abscissa and far to the left of the vertical ordinate, so that the pattern only appears to be parallel. The test is to study the reaction in both directions. A true ping-pong mechanism will give rise to parallel initial velocity patterns in each direction, whereas an apparent ping-pong mechanism will show a parallel pattern in one direction and an intersecting pattern in the other.

4. Obtaining the Values of Parameters

 The plotting of initial velocity data as described above is useful for determining the function to which the kinetic data should be fitted by nonlinear regression analysis (12), which should be used to obtain estimates of the values of kinetic parameters, and for illustrating the agreement between the experimental data and theoretical fit. Determination of values for kinetic parameters, together with estimates of their standard errors, should come from the fit of all the data to an assumed rate equation.

References

1. W. W. Cleland (1963) Biochim. Biophys. Acta 67, 104–137. 

2. W. B. Knight and W. W. Cleland (1989) Biochemistry 28, 5728–5734.

3. K. Dalziel (1975) The Enzymes 11, 1–60. 

4. H. Theorell and B. Chance (1951) Acta Chem. Scand. 5, 1127–1144. 

5. J. F. Morrison and K. E. Ebner (1971) J. Biol. Chem. 246, 3977–3984.

6. J. F. Morrison and E. Heyde (1972) Ann. Rev. Biochem. 41, 29–54. 

7. P. A. Frey (1992) The Enzymes 20, 141–186. 

8. E. S. Snell and S. J. Di Mari (1970) The Enzymes 2, 335–370. 

9. E. Garces and W. W. Cleland (1969) Biochemistry 8, 633–640. 

10. D. Northrop (1969) J. Biol. Chem. 244, 5808–5819. 

11. W. W. Cleland (1986) Invest. Rates Mech. Reactions 6, 791–870. 

12. W. W. Cleland (1979) Meth. Enzymol. 63, 103–138.