
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 17-3-2016
التاريخ: 2-3-2016
التاريخ: 6-3-2016
التاريخ: 14-3-2016
|
فضاء المتجهات الحقيقي:
درسنا في السابق فضاء المتجهات الإقليدي . سنحاول في هذا الفصل تسليط الضوء على فضاءات أخرى إضافة للفضاء الإقليدي مثل المصفوفات ومتعددات الحدود وغيرها.
تعريف (1-1):
تسمى المجموعة غير الخالية V مع عمليتين ثنائيتين معرفتين هما الجمع والضرب بعدد ثابت، فضاء متجهات على الأعداد الحقيقية، إذا تحقق الشروط الآتية:

ملاحظة:
1- عملية الجمع يرمز لها + والضرب بعدد ثابت يعني ضرب v بالعدد k (أي kv).
2. تسمى عناصر V متجهات.
3. الرمز A1 استخدم هنا لشروط الجمع، أما m1 فقد استخدمت للضرب (لسهولة حفظها).
مثال(1):
المجموعة V=Rnمع عمليتي الجمع والضرب بعدد ثابت والمعرفة في (1.1) تحقق الشروط أعلاه. عليه فهي قضاء متجهات.
مثال(2): لتكن {0}V = ، أي أن V تحوي على عنصر واحد هو 0، فإن V تحقق شروط ( 1-1) جميعها فهي إذن فضاء متجهات.
مثال(3):
لتكن V={(a,b):b=ka} حيث k عدد حقيقي ثابتة و a عدد حقيقي. عليه فإن V تحتوي على جميع النقاط الواقعة على الخط المستقيم b = ka المار بنقطة الأصل والذي ميله k ولما كان
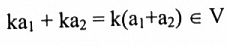
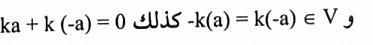
فإن الشرطان A1 و A5 متحققان. بما أن بقية الشروط يمكن إثباتها بسهولة. لذا فإن V فضاء متجهات.
مثال(4):
نفرض {y:y = 2x + 1 } V = حيث x عدد حقيقي. لاحظ أن V مجموعة جميع النقاط الواقعة على الخط المستقيم V .y = wx+1 لا تكون فضاء متجهات لأن شرط الأنغلاق الجمعي لا يتحقق وذلك لأن:
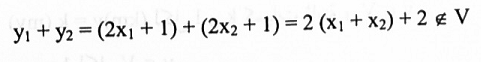
مثال(5):
لتكنV=P n(x)مجموعة جميع متعددات الحدود من الدرجة أصفر أو تساوي n. أي:
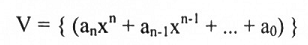
حيث ai أعداد حقيقية. فإن V فضاء متجهات لأن:

الشرط As متحقق. بالاستمرار على نفس الطريقة يمكننا برهان الشروط الاخرى. إذن V=P n(x). فضاء متجهات.
مثال(6):
إذا كانت 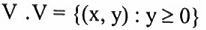 . فإن مجموعة جميع النقاط في R2 التي تكون الربعين الأول والثاني K ليست فضاء متجهات لأن على سبيل المثال ، النقطة (1,1) ليست لها معكوس في V V] ∌ -1,-1)].
. فإن مجموعة جميع النقاط في R2 التي تكون الربعين الأول والثاني K ليست فضاء متجهات لأن على سبيل المثال ، النقطة (1,1) ليست لها معكوس في V V] ∌ -1,-1)].
مبرهنة (1-2):
لتكن V فضاء متجهات، v∊V و K كمية ثابتة، فإن :
1. 0V = 0
2. K0 = 0
3. (-1) v = -v
4. إذا kv = 0 فإن K = 0 او v = 0
البرهان:
نبرهن (2) و (3).
2. بما أن 0 + 0 = 0 [A4 مبرهنة (1-1) ].
إذن k (0+0) = K0 + ko = K0 [m3 مبرهنة (1-1) ].
بإضافة –k0 للطرفين:




|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|