When you borrow money at compound interest and make regular repayments,  interest is normally calculated on the amount you owe. Usually the interest is calculated at the time your payment is due; when you buy a house on a mortgage and make monthly payments, the interest is compounded monthly. There is a penalty for late payments, in addition to the interest on the missed payment. Usually there is no reward for paying early in the month. We shall refer to this arrangement as a standard compound interest loan, or simply a compound interest loan.

To clarify this, suppose your house payment of $2,000 is due on the first of the month, and on June 1st this year your total indebtedness is $100,000. For simplicity,  say your annual interest rate is 12%, so the interest for 1 month is 1%. On July 1st, interest of $1,000 (1% of $100,000) is added to your debt. Then payments are credited. Assuming you made the standard $2,000 payment, this is subtracted from your debt, which becomes($100,000+$1,000−$2,000)= $99,000. When August 1st comes around, the new interest will be $990 (1% of $99,000). It does not matter when you made the payment, provided it is on or before July 1st; even if you paid on June 2nd, it is applied on July 1st. If you made a payment greater than $2,000 during June, the total would be subtracted from your debt on July 1st.

If you miss a payment, or pay less than $2,000, some penalty is exacted. The arrangements differ from loan to loan. Some lenders charge a higher interest rate on the amount in arrears; some charge a fee; many do both.

The amount of payment required to pay off a loan can be calculated from the data about the loan.

The calculation proceeds as follows. Say you borrow $P at M% monthly interest  (compounded monthly), and pay it back at the end of Y years. The arithmetic is the same as if you put $D into a savings account each month at M% interest compounded monthly, and at the end of Y years you have exactly enough money to pay off your loan. This amount is $P(1 + m)ⁿ, where n = 12Y and m = M/100.

Then the required monthly payment is $D.

The only difference between this and the example of accumulated savings is that loan repayments usually start at the end of the first month, so for Y years the total number of months for which your money accumulates is 12Y − 1, not 12Y, and you gain nothing during the first month. If we continue to write n for the number of months in the life of the loan, we use n − 1 in place of n in the accumulation formula. This actually simplifies the formula: we want to sum

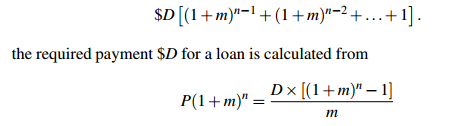
Sample Problem 1.1 You take out a compound interest loan of $100,000 at 6% annual interest to pay off your house. The period is 30 years. What payment is required each month?

Solution. Suppose the monthly payment is $D. The interest rate is .5% = .005 per month. There are 360 months in 30 years. So P(1+m)n is

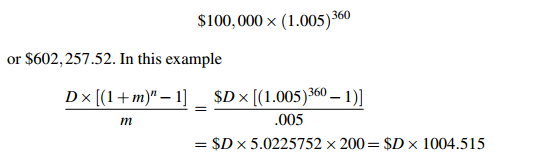
so D × 1004.515 = 602,257.52 and D = 599.55. You would pay $599.55 per month.

It is interesting to observe the differences that follow from small changes in a long-term loan. Suppose we change the annual rate of interest in the preceding example from 6% to 8%, leaving the principal and period unchanged. The interest rate is .00666... or 1/150 per month. So the accumulation after 30 years at 8% is

                                      $100,000×(151/150) ³⁶⁰

or $1,093,572.96. In the “regular savings” model, depositing $D per month, your accumulated savings would be

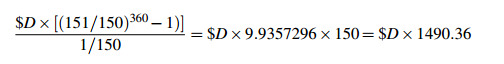
So your monthly payment is D = 733.76.

On the other hand, changing the period of the loan makes less difference than you might think. Reducing the period by 20%, to 24 years, adds less than 10% to your monthly payment:

Sample Problem 1.2 You take out a compound interest loan of $100,000 at 6% annual interest to pay off your house. The period is 24 years. What payment is required each month?

Solution. As in Sample Problem 15.2, the interest rate is .5% = .005 per month.

There are 288 monthly payments. So in this case P(1+m)ⁿ is

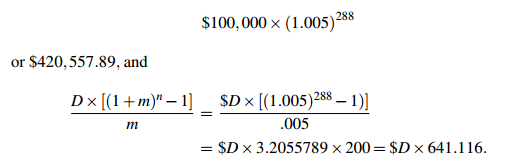
So D×641.116 = 420,557.89. You would pay $655.98 per month

Here is another way of interpreting the above calculation: suppose you contracted to buy your $100,000 house at 6% annual interest over 30 years. Your bank requires a monthly payment of $600 (actually $599.55 per month, but banks often round up slightly, and reduce the last payment a little). If you decided to pay an extra $56 each month, you would finish paying for your house 6 years ahead of schedule.

We have calculated D from A (answering the question “What payment must I make?”). We can also calculate A from D (“Given the maximum payment I can make, how much can I afford?”)

Sample Problem 1.3 You want to buy a car. You can get an 8% loan over 5 years. You can pay $200 per month. How much can you afford to pay for the car?

Solution. m = 8/12% = 1/150,D = 200,n = 60. So

                                 mP(1+m)ⁿ = D×[(1+m)ⁿ −1]

becomes

                         P(151/150) ⁶⁰/150 = 200[(151/150) ⁶⁰−1],