de Sitter Cosmology

de Sitter space holds special interest because of its close connection with observational cosmology. The model of cosmology which is presently gaining the status of a “standard model” involves de Sitter space in two ways. First it is believed that the early universe underwent an epoch of rapid inflation during which the space-time geometry was very close to de Sitter. The inflationary theory is more than two decades old and by now has been well tested.

More recently de Sitter space has entered cosmology as the likely candidate for the final fate of the universe. The history of the universe seems to be a transition from an early de Sitter epoch in which the vacuum energy or cosmological constant was very large to a late de Sitter phase characterized by a very small but not zero cosmological constant. de Sitter space is the solution of Einstein's field equations with a positive cosmological constant that exhibits maximal symmetry. Four-dimensional de Sitter space may be defined by embedding it in (4 + 1) dimensional flat Minkowski space. It is the hyperboloid given by

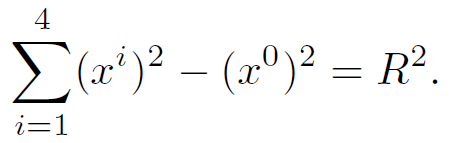 (1.1)

The radius of curvature R is related to the cosmological constant, λ.

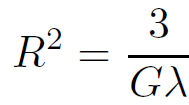 (1.2)

de Sitter space can also be written in the form

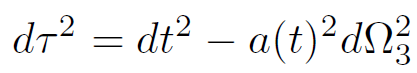(1.3)

where dΩ²₃ is the metric of a unit 3-sphere, and the scale factor a is given by

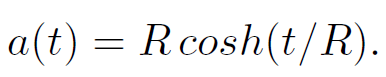 (1.4)

For our purposes we want to put this in a form that will allow us to read off the Penrose diagram. To that end define the conformal time T by

 (1.5)

One easily finds that the geometry has the form

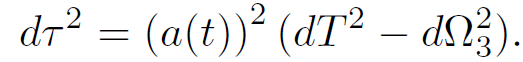 (1.6)

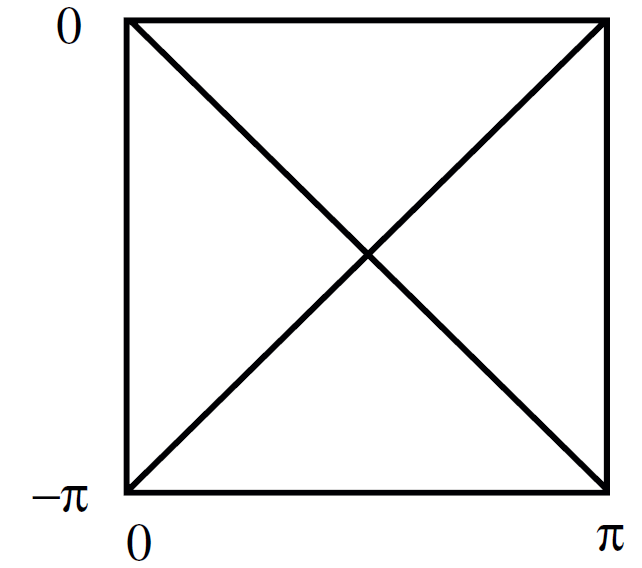
Fig. 1.1. Penrose diagram for de Sitter space-time.

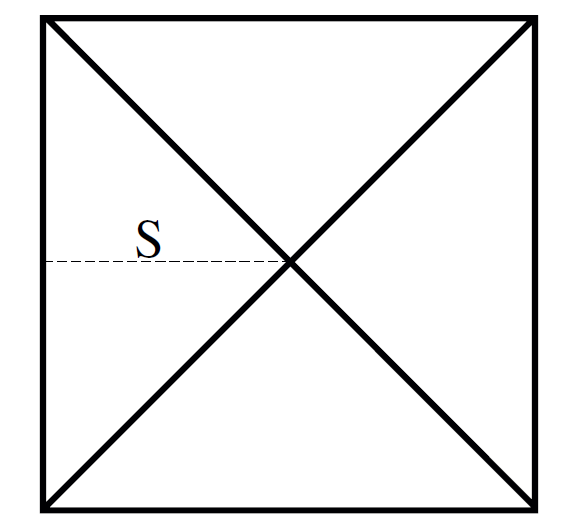
Fig. 1.2. Extremal space-like surface in de Sitter space-time.

Furthermore when t varies between ±∞, the conformal time  (T = tan⁻¹ (tanh(t/R)) -π/2) varies from −π to 0.Since the polar angle on the sphere also varies from 0 to π the Penrose diagram is a square as in Figure 1.1.

Once again the Bousso construction divides the Penrose diagram into four quadrants. However, the contracting light sheets in the upper and lower quadrants are oriented oppositely to the usual F.R.W. case. The reason is that the geometry rapidly expands as we move toward the upper and lower boundary of the de Sitter space.

Of particular interest is the bound on a space-like surface beginning at the center of the Penrose diagram and extending to the left edge as in Figure 1.2. We leave it as an exercise to show that the entropy is

Fig. 1.3. Inflationary universe.

bounded by the area of the 2-sphere at the center of the diagram. In fact the maximum entropy on any such surface is given by

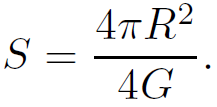 (1.7)

de Sitter space has a special importance because of its role during the early evolution of the universe. According to the inflationary hypothesis, the universe began with a large vacuum energy which mimicked the effects of a positive cosmological constant. During that period the geometry was de Sitter space. But then at some time the vacuum energy began to decrease and the universe made a transition to an F.R.W. universe. The transition was accompanied by the production of a large amount of entropy, and is called reheating.

Inflationary cosmology is illustrated in Figure 1.3. In order to construct the Penrose–Bousso diagram we begin by drawing Penrose diagrams for both de Sitter space and either radiation or matter dominated F.R.W. The Penrose–Bousso diagram for de Sitter space is shown in Figure 1.4. In order to describe inflationary cosmology we must terminate the de Sitter space at some late time and attach it to a conventional F.R.W. space as in Figure 1.5. The dotted line where the two geometries are joined is the reheating surface where the entropy of the universe is created.

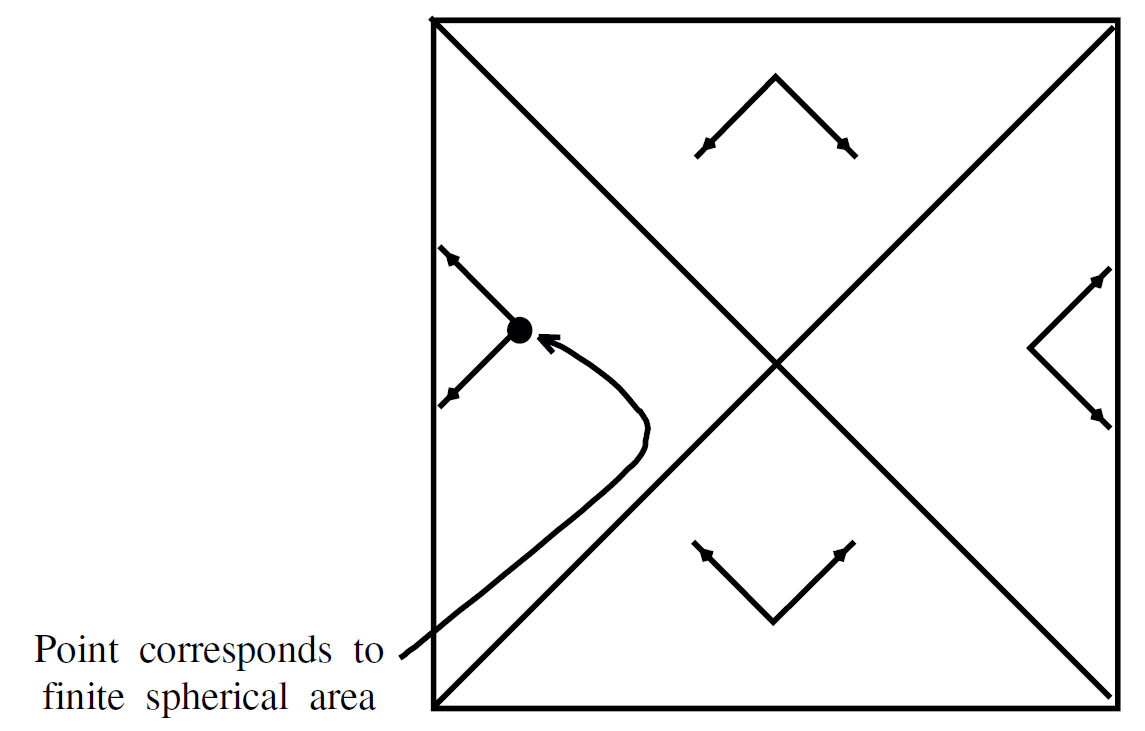
Fig. 1.4. Buosso wedges for de Sitter geometry.

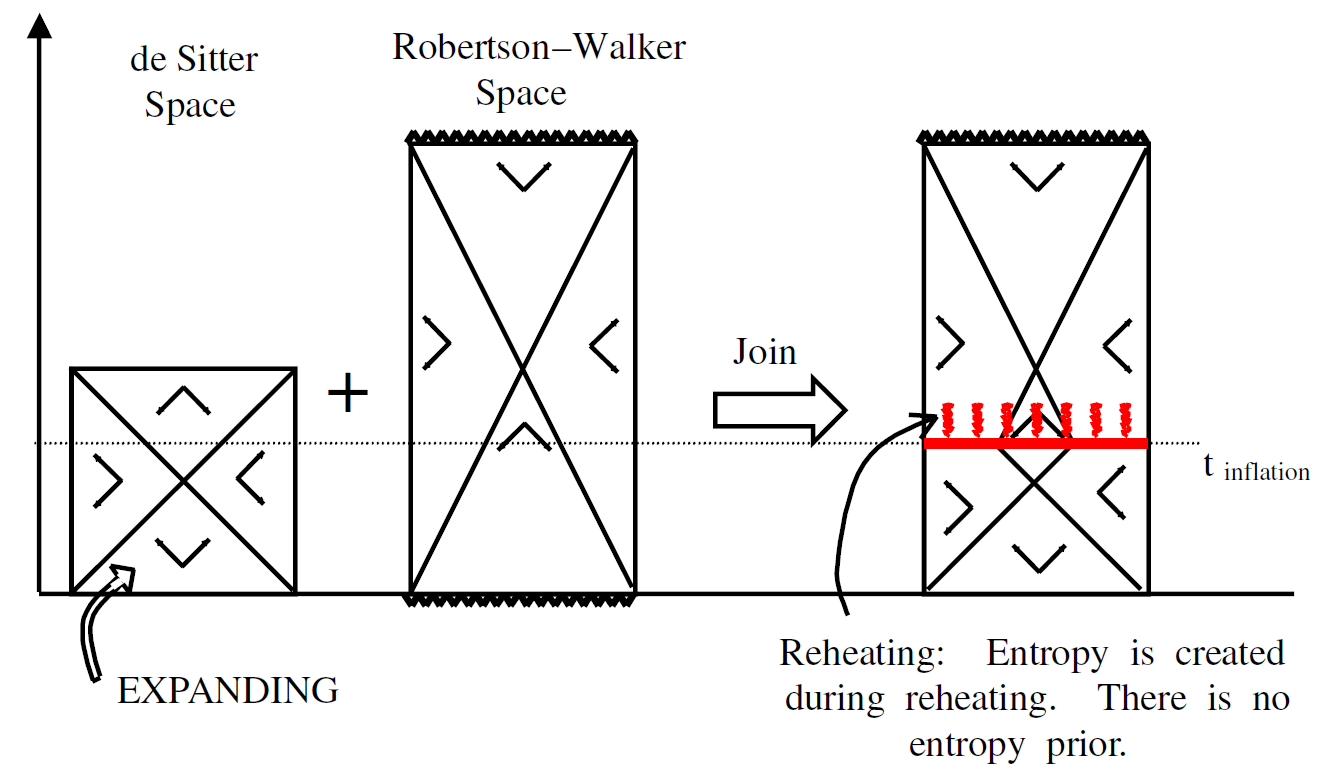
Fig. 1.5. Joining of inflationary and post-inflationary geometries.

Let us focus on the point p in Figure 1.6. It is easy to see that in an ordinary inflationary cosmology p can be chosen so that the entropy on the space-like surface p - q is bigger than the area of p. However Bousso's rule applied to point p only bounds the entropy on the past light sheet.

Fig. 1.6. Entropy bound on spherical region causally connected to inflationary period.

In this case most of the newly formed entropy on the reheating surface is not counted since it never passed through the past light sheet. Typical inflationary cosmologies can be studied to see that the past light sheet bound is not violated.