


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 15-11-2015
التاريخ: 29-12-2015
التاريخ: 29-12-2015
التاريخ: 7-1-2016
|
والقطاع الدائري جزء من سطح دائرة محدود بقوس ونصف قطرين كما في الشكل.
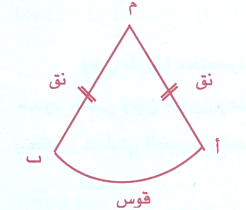
حيث م مركز الدائرة
نق نصف قطرها .
أ ب قوس من الدائرة.
ومساحة القطاع تعتمد على مقدار قياس زاوية رأسه ــ الزاوية المركزية  أ م ب كما في الشكل
أ م ب كما في الشكل
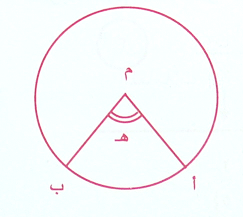
هـ مساحة القطاع
اي ان ــــــــــ = ـــــــــــــــــــــ
360 مساحة الدائرة
هــ مساحة القطاع أ م ب
أي ان ــــــــــ = ـــــــــــــــــــــــــــ
360 نق2π
ومنها مساحة القطاع = هـ○360○ × نق2 π
فمساحة القطاع الذي نصف قطر الدائرة المأخوذة منها 8 سم وقياس زاويته المركزية 60 هي :
60 32
مساحة القطاع = ـــــــــــــــــ × 8 × 8 × π = ـــــــــــ π وحدة مساحة .
360 3
هذا ويمكن إيجاد القطاع الدائري بالقانون :
مساحة القطاع = 12نق2هـ2 ، حيث هـ بالتقدير الدائري (راديان) وطول قوسه 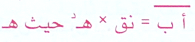 بالتقدير الدائري ( راديان)
بالتقدير الدائري ( راديان)



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|