المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | اقتران خطي Linear Function |
 5216
 01:44 صباحاً
التاريخ: 29-10-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 39-40|
أقرأ أيضاً
التاريخ: 23-12-2015
8872
التاريخ: 29-11-2015
2719
التاريخ: 27-10-2015
1606
التاريخ: 14-11-2015
1408
|
اقتران كثير حدود , قاعدته ق(س) = أس + ب , لكل أ,ب∊ح أ≠صفر , حيث أس س يساوي الواحد الصحيح ومنحناه بمثل بخط مستقيم ومن الدرجة الأولى منحناه كما في الشكل :
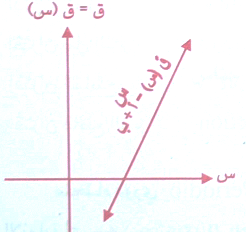
وهناك اقتران كحالة خاصة من الاقتران الخطي يسمى اقتران محايد Identity Function قاعدته ق(س) = س ومنحناه يمر بنقطة الأصل كما في الشكل .
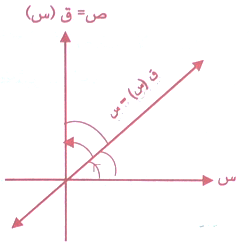
وفيه قيمة المتغير المستقل س = قيمة المتغير التابع ص كما في الجدول :
وعند تمثيل هذا الجدول بيانياً فينتج الشكل السابق .
|
|
|
|
علامات تحذيرية قد تسبق الموت القلبي المفاجئ لدى الشباب
|
|
|
|
|
|
|
استنساخ ذئاب عملاقة وشرسة "انقرضت منذ آلاف السنين"
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
