


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-06-24
التاريخ: 13-5-2017
التاريخ: 9-3-2016
التاريخ: 2023-06-15
|
ذكرنا منذ قليل أن المعادلة التي تصف تطور الدالة الموجية 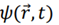 مع الزمن، تسمى بمعادلة شرودنغر. ان هذه المعادلة هي عصب ميكانيكا الكم وتناظر بالضبط قانون نيوتن الثاني في الميكانيكا الكلاسيكية، والذي يصف تطور حالة الجسم العادي مع الزمن.
مع الزمن، تسمى بمعادلة شرودنغر. ان هذه المعادلة هي عصب ميكانيكا الكم وتناظر بالضبط قانون نيوتن الثاني في الميكانيكا الكلاسيكية، والذي يصف تطور حالة الجسم العادي مع الزمن.
أحد فروض ميكانيكا الكم الأساسية ينص على (لكل كمية فيزيائية يمكن قياسها، هناك مؤثر أو معامل operator مناظر لها) مثلا مركبة كمية الدفع الخطية px لها مؤثر مناظر هو 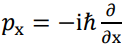 ، حيث 1–√ = i نلاحظ أن المؤثر يحتوي على عملية رياضية وهي الاشتقاق. المؤثر المناظر لطاقة الوضع (الجهد) هو نفسه أي
، حيث 1–√ = i نلاحظ أن المؤثر يحتوي على عملية رياضية وهي الاشتقاق. المؤثر المناظر لطاقة الوضع (الجهد) هو نفسه أي 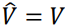 . مؤثر الطاقة الكلية هو
. مؤثر الطاقة الكلية هو 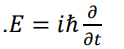
الآن، نعلم من قوانين الفيزياء الكلاسيكية أن الطاقة الكلية لأي جسم تساوي طاقة الحركة مضافا إليها طاقة الوضع:
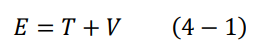
نضع الآن المؤثرات المناظرة لكمية الدفع والجهد والطاقة الكلية، مع استخدام
p2/2m = T، ثم نقوم بضرب الطرفين ب ψ:
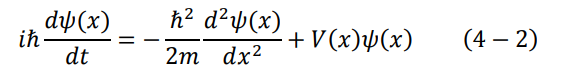
وهذه هي معادلة شرودنغر الشهيرة، في بعد واحد وهو x. وكما نرى هي معادلة تفاضلية من الدرجة الثانية.
تلعب هذه المعادلة نفس الدور الذي يلعبه قانون نيوتن الثاني F = ma، في الميكانيكا الكلاسيكية. فلو تحرك جسم في اتجاه x مثلا، فاننا نستطيع التنبؤ بموقعه عند أي لحظة من الزمن، اذا ما علمنا شروطه الابتدائية بنفس الطريقة تحدد معادلة شرودنغر تطور الدالة ψ عند أي لحظة من الزمن، بمعلومية الشروط الابتدائية، ولكن بالحدود التي يسمح بها مبدأ عدم اليقين.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|