
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
ما شكل الكون؟
المؤلف:
بول ديفيز
المصدر:
الجائزة الكونية الكبرى
الجزء والصفحة:
الفصل الثاني (ص59 – ص61)
2023-03-08
1571
ما شكل الكون؟
المؤلف/ بول ديفيز
الكتاب/ الجائزة الكونية الكبرى
الفصل والصفحة/ الفصل الثاني (ص59 – ص61)
كل هذا مقبول تماما، لكن هل كان أينشتاين محقًا بالفعل في تصوره للكون على شكل كرة فائقة؟ هنا، يقدم لنا المسبار WMAP عونًا كبيرًا من البديهي أنه لو كان الكون يفتقر للتطابق في الشكل بدرجة كبيرة، لبدا هذا واضحًا في أنماط الموجات الميكروية الآتية من السماء. إلا أن حقيقة اتساق أنماط الإشعاع في الشكل لهذه الدرجة توحي بأن الكون بقدر ما يمكننا رصده - ذو شكل منتظم.13 لكن ما هذا الشكل؟ بالعودة للتشبيه ثنائي الأبعاد يمكننا تحديد شكلين منتظمين بشكل تام؛ السطح الممتد اللانهائي، والكرة تامة الاستدارة. إلا أن هناك نوعًا ثالثًا أشبه بالكرة المقلوبة. تذكر أنه على سطح الكرة يكون مجموع زوايا المثلث أكثر من 180 درجة من الناحية الفنية يقال إن الكرة منحنية بشكل «موجب». لكن ماذا عن السطح المتسق الذي فيه يكون مجموع زوايا المثلث أقل من 180 درجة؟ مثل هذا الشكل يكون له تقوس «سالب». مثل هذا السطح الذي سيبدو كالسرج، يمكن أن يوجد، لكنه سيمتد إلى ما لا نهاية (انظر الشكل 2-8). إن الأسطح الثلاثة - ذات التقوس الصفري والموجب والسالب - يمكن تعميمها إلى ثلاثة أبعاد. ومنذ عشرينيات القرن العشرين، حين أدرك علماء الكونيات لأول مرة أن هناك ثلاثة أشكال متباينة للفضاء ذي الشكل المتطابق المتسق، يرغب العلماء في معرفة أي منها الأقرب شبها بكوننا.
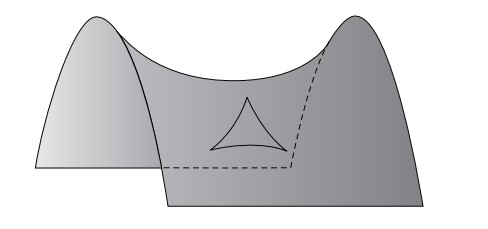
شكل 2-8: الفضاء المنحني السالب. من الممكن بالمعايير الكونية، أن يكون الفضاء متطابقا، لكنه منحن إلى الخارج وليس إلى الداخل الشكل ثنائي الأبعاد المبين هنا يعد تمثيلا لهذا الفضاء ثلاثي الأبعاد المنحني بالسلب. إنه فضاء لانهائي ومتجانس. تعبر هندسة الانحناء السالب عن نفسها عن طريق تشويه شكل المثلث المرسوم الذي يكون مجموع قياس زواياه أقل من 180 درجة.
جرت محاولات عدة للتعامل تعاملا مباشرا مع هذه المشكلة، فلأن هندسة الأشكال مع الثلاثة للفضاء متباينة فينبغي أن يصير علماء الفلك قادرين على التمييز بينها بسهولة وبالنظر فقط. إن قياس زوايا مثلث عبر مسافات كونية ليس بالأمر الممكن، إلا أن هناك احتمالات أخرى بالعودة مجددًا إلى العالم ثنائي الأبعاد، تخيل أنك رسمت عددًا من الدوائر متحدة المركز على ورقة مستوية. إن المساحة التي تشغلها كل دائرة منها تزيد بالتناسب مع مربع نصف قطرها، وإذا ضاعفت نصف القطر تتضاعف مساحة الدائرة أربع مرات. لكن على السطح الكروي تصير هذه العلاقة مغلوطة؛ إذ تزيد المساحة مع زيادة نصف القطر بمعدل أقل من اليسير رؤية ذلك؛ لأنك لو حاولت فرد قبعة فسيكون عليك قص أجزاء مثلثة منها، وبهذا لن تغطي المساحة التي يغطيها نصف قطرها على سطح مستو. وبالمثل، ستزيد مساحة شكل السرج بمعدل أكبر من مربع نصف القطر. بالانتقال إلى عالم الأبعاد الثلاثية سنجد أن حجم أي منطقة في الفضاء سيزيد بقدر يساوي مكعب نصف قطر هذه المنطقة لو أن الفضاء مستو (مستو لكن ثلاثي الأبعاد، تذكر، وليس مسطحًا تمامًا). أما لو كان الفضاء على شكل كرة فائقة، كما اقترح أينشتاين، فسيزيد الحجم بمعدل أقل مع زيادة نصف القطر، ولكنه لو كان على شكل «السرج الفائق فسيزيد بمعدل أكبر. ومن الممكن حساب حجم أي منطقة في الفضاء بحساب عدد المجرات التي تحتوي عليها.
حاول بعض علماء الفلك تأسيس هندسة الكون على هذا النمط، لكن نتائجهم لم تكن حاسمة بسبب صعوبة قياس المسافات الدقيقة التي تفصلنا عن المجرات البعيدة وغير ذلك من الصعوبات التقنية. ومع ذلك فمن الممكن الحصول على إجابة من البيانات الخاصة بالمسبار WMAP، وذلك بقياس حجم التفاوت في درجات الحرارة، البقع الحارة والباردة (الفاتحة والداكنة). قبل إطلاق القمر الصناعي الحامل للمسبار WMAP، كان المنظرون قد توصلوا بالفعل إلى الحجم الفعلي للتفاوت في درجات الحرارة، لكن تحويل ذلك إلى حجم زاوي واضح في السماء يعتمد على هندسة الفضاء: فإذا كان الفضاء موجب الانحناء فسيجعل هذا الزوايا تبدو أكبر، في حين الانحناء السالب سيجعلها أصغر. أما لو كان الفضاء مستويًا (أي يتبع الهندسة الإقليدية) فسيكون الحجم الزاوي للتفاوت بين أقوى النقاط الحارة والباردة حوالي درجة واحدة عرضًا. كانت النتائج التي وردتنا من القمر الصناعي حاسمة؛ 14 إذ كان التفاوت بالفعل قريبا من درجة واحدة في الحجم، وهي النتيجة التي أكدتها التجارب التي جرت على الأرض وعن طريق المناطيد. وقد أعلن علماء الكونيات وقتها أن الفضاء - ضمن نطاق دقة رصد قدره 2 بالمائة - مستو.15
هوامش
(13) To sound a note of caution, some cosmologists are concerned that the largest features mapped by WMAP (technically, the lowest multipoles) display some oddities not predicted by the conventional big bang model of the universe. It is too soon to know whether this is due to problems with the equipment and/or data analysis or if it points to something significant and unexpected about the structure of the universe.
(14) The limited accuracy of these observations cannot establish that the universe is exactly flat. What they tell us is that if the universe is shaped like Einstein’s hypersphere, then the radius of the hypersphere is exceedingly large, so that within the volume of space probed by our instruments we cannot discern any curvature. Similar remarks apply to any negative curvature.
(15) Even if space is flat, it need not necessarily be infinite. That is because Einstein’s theory says nothing about the topology of space. One possible topology involves identifying points. Think of a sheet of paper on which a particle enters from the left, traverses the paper, and exits from the right. Now imagine rolling up the paper and gluing the left and right edges together. The particle that previously exited from the right would now reappear from the left. Some cosmologists have suggested that space might be like this and resemble a hall of mirrors. If we inhabited such a universe, it might look to us at first sight as if “the hall of mirrors” extended to infinity, but on closer inspection we would discover that a finite volume of space repeats itself, infinitely often. It is possible that the universe consists of three-dimensional cells, repeated periodically, and that light which we take to be from far away is in fact wrapping around one or more times, creating the illusion of distance. More complicated shapes, such as the three-dimensional analogue of the surface of a segmented soccer ball, have also been suggested.
 الاكثر قراءة في مواضيع عامة في علم الفلك
الاكثر قراءة في مواضيع عامة في علم الفلك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















