


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-3-2022
Date: 5-4-2022
Date: 30-3-2022
|
 |
 |
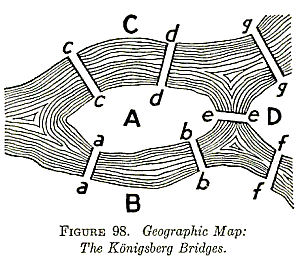
The Königsberg bridge problem asks if the seven bridges of the city of Königsberg (left figure; Kraitchik 1942), formerly in Germany but now known as Kaliningrad and part of Russia, over the river Preger can all be traversed in a single trip without doubling back, with the additional requirement that the trip ends in the same place it began. This is equivalent to asking if the multigraph on four nodes and seven edges (right figure) has an Eulerian cycle. This problem was answered in the negative by Euler (1736), and represented the beginning of graph theory.
 |
 |
On a practical note, J. Kåhre observes that bridges 











Biggs, N. L.; Lloyd, E. K.; and Wilson, R. J. Graph Theory 1736-1936. Oxford, England: Oxford University Press, 1976.
Bogomolny, A. "Graphs." http://www.cut-the-knot.org/do_you_know/graphs.shtml.Chartrand, G. "The Königsberg Bridge Problem: An Introduction to Eulerian Graphs." §3.1 in Introductory Graph Theory. New York: Dover, pp. 51-66, 1985.
Euler, L. "Solutio problematis ad geometriam situs pertinentis." Comment. Acad. Sci. U. Petrop. 8, 128-140, 1736.
Reprinted in Opera Omnia Series Prima, Vol. 7. pp. 1-10, 1766.
Harary, F. Graph Theory. Reading, MA: Addison-Wesley, pp. 1-2, 1994.
Kåhre, J. "K:)nigsberg Bridges Solved." http://www.matheory.info/konigsberg/.Kraitchik, M. §8.4.1 in Mathematical Recreations. New York: W. W. Norton, pp. 209-211, 1942.
Newman, J. "Leonhard Euler and the Königsberg Bridges." Sci. Amer. 189, 66-70, 1953.
Pappas, T. "Königsberg Bridge Problem & Topology." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 124-125, 1989.
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 192, 1990.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 256-259, 1999.Wilson, R. J. "An Eulerian Trail through Königsberg." J. Graph Th. 10, 265-275, 1986.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|