The Spencer-Brown form is a simple mathematical concept that formalizes what a mathematical object is formally identical to what it is not (Spencer-Brown 1997, pp. ix and 180). The Spencer-Brown form is defined by two primitive equations which are its axioms (Spencer-Brown 1969):

1. Condensation: Two instances of the form are equivalent to one instance of the form if they are placed in the same space.

2. Cancellation: Two instances of the form are equivalent to no instance of the form alias empty space if one of the forms is the argument of the other form.

This cancellation is of particular interest because it permits bootstrapping of a binary domain and a binary range for the form function from itself. Hence empty space can be represented as a form taking itself as its argument, and can thus be called the inverse of itself.

The traditional notation for the form is a kind of vinculum token that spans its arguments thus offering a bracket-free notation that is always syntactically correct. Nested circles or rectangles and graphs offer alternative ways of representing form expressions (Spencer-Brown 1969). Notations that use nested brackets have been used by various authors (c.f. Meguire 2003).

Arguments of the form can be either explicit instances of the form itself (primary arithmetic) or collections of arguments that are variables defined as representing either the form or the empty space obtained by processing a form by a form (primary algebra). Arithmetic form expressions involving only constants simplify instantly. Algebraic form expressions involving variables can be evaluated by enumerating and testing all possible replacements of these variables. These primary definitions define an abstract algebra and can be used to reconstruct numbers and operations of an algebra over an infinite field of integers.

The Spencer-Brown form can hence be regarded as a symbol for a distinction which takes itself as its own domain to generate the range for functions it represents and operates on. Contrary to some interpretations the form is not equivalent to NAND, the Peirce "cut" in a sheet of assertion, or the Sheffer stroke, because it starts from empty space, uses itself as its argument and because each form token accepts an arbitrary number of constant, variable or recursively reentrant arguments.

The form approach has been adopted as a formal resource of for instance a sociologic theory systems (Luhmann 1996). On the other hand it has also been criticized as inconsistent (Cull et al. 1979), but it turns out that arbitrary nested form token can be evaluated automatically in the Wolfram Language if brackets for form tokens are replaced by DiscreteDelta (Schreiber 2003).

Numbers can be represented as forms following either the original interpretation given by Spencer-Brown (1957), by adding further axioms and tokens not included in the original system (James 1993), or by relating form expressions to their corresponding Wolfram rule numbers (Schreiber 2004). This third approach is able to handle arbitrary integers or Boolean algebras of degree 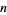 in general, and to reconstruct the 256 binary cellular automaton rules (Wolfram 1983, 2002) from 26 Spencer-Brown forms in particular. Large numbers can be represented efficiently by constructing form expressions which specify only positions of ones.

A form expressions can process results of its own operation as input recursively. Varela (1975, pp. 5-24) proposed to extend the domain and the range of the form by including an "autonomous state" as a symbol for this imaginary value which according to that so-called "extended calculus of indication" would not change its value when processed by the form. The obvious problem of this modification is that the form could not draw a distinction between two autonomous states. While this could be handled by postulating a fourth state which differs from the autonomous state in phase it is possible to avoid such complication. This can be demonstrated by using form reentry to add two infinite length sequences of forms (Schreiber 2004).

REFERENCES:

Cull, P. and Frank, W. "Flaws of Form." Int. J. General Systems 5, 201-211, 1979.

Houser, N.; Eller, J.; Lewis, A. C.; de Tienne, A.; de Waal, C.; Kaposta, J.; Morton, L. H.; and Rujuwa, M. "Peirce Edition Project." http://www.iupui.edu/~peirce/.

James, J. M. "A Calculus of Number Based on Spatial Forms." Thesis. University of Washington, 1993. http://www.lawsofform.org/docs/jjames-thesis.txt.

Kauffman, L. H. "The Mathematics of Charles Sanders Peirce." Cybernetics and Human Knowing 8, 79-110, 2001.

Keenan, D. and James, J. "Laws of Form Bibliography." http://www.lawsofform.org/bib/.

Keenan, D. ad Whitaker, R. "Laws of Form Bibliography." http://www.enolagaia.com/GSBBib.html.

Luhmann, N. "Soziale Systeme, Grundriß einer allgemeinen Theorie." Frankfurt am Main, Germany: Suhrkamp, 1996.

Meguire, P. "Discovering Boundary Algebra: A Simple Notation for Boolean Algebra and the Truth Functions." Int. J. General Systems 32, 25-87, 2003.

Schreiber, M. "Universal Form." Poster. New Kind of Science Conference 2003 in Boston.

Schreiber, M. "Computational Equivalence: Form 110." Proc. New Kind of Science Conference 2004 in Boston. http://www.wolframscience.com/conference/2004/presentations/material/mschreiber-computational.nb.

Sheffer, H. M. "A Set of Five Independent Postulates for Boolean Algebras, with Application to Logical Constants." Trans. Amer. Math. Soc. 14, 481-488, 1913.

Shoup, R. "Collection of Laws of Form Materials, 2000-2004." http://www.lawsofform.org/collection.html.

Spencer-Brown, G. Probability and Scientific Inference. London: Longmans, Green & Co, 1957.

Spencer-Brown, G. Laws of Form. London: Allen & Unwin. 1969.

Spencer-Brown, G. "An Algebra for the Natural Numbers." In Gesetze Der Form. Lübeck, Germany: Bohmeier, 132-138, 1997.

Varela, F. "A Calculus for Self-Reference." Int. J. General Systems 2, 5-24, 1975.

Wolfram, S, "Statistical Mechanics of Cellular Automata." Rev. Modern Phys. 55, 601-644, 1983.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد