


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-2-2016
Date: 2-1-2022
Date: 14-2-2017
|
Let 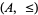 and
and 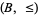 be disjoint totally ordered sets with order types
be disjoint totally ordered sets with order types 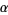 and
and 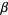 . Then the ordinal sum is defined at set
. Then the ordinal sum is defined at set 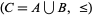 where, if
where, if 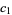 and
and 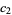 are both from the same subset, the order is the same as in the subset, but if
are both from the same subset, the order is the same as in the subset, but if 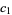 is from
is from 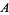 and
and 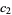 is from
is from 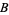 , then
, then 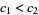 has order type
has order type 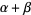 (Ciesielski 1997, p. 48; Dauben 1990, p. 104; Moore 1982, p. 40).
(Ciesielski 1997, p. 48; Dauben 1990, p. 104; Moore 1982, p. 40).
One should note that in the infinite case, order type addition is not commutative, although it is associative. For example,
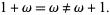 |
(1) |
In addition, 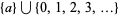 , with
, with 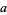 the least element, is order isomorphic to
the least element, is order isomorphic to 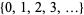 , but not to
, but not to 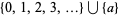 , with
, with 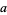 the greatest element, since it has a greatest element and the other does not.
the greatest element, since it has a greatest element and the other does not.
An inductive definition for ordinal addition states that for any ordinal number 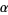 ,
,
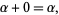 |
(2) |
and
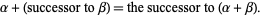 |
(3) |
If 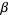 is a limit ordinal, then
is a limit ordinal, then 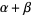 is the least ordinal greater than any ordinal in the set
is the least ordinal greater than any ordinal in the set 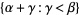 (Rubin 1967, p. 188; Suppes 1972, p. 205).
(Rubin 1967, p. 188; Suppes 1972, p. 205).
REFERENCES:
Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Moore, G. H. Zermelo's Axiom of Choice: Its Origin, Development, and Influence. New York: Springer-Verlag, 1982.
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|