


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-1-2022
Date: 14-2-2017
Date: 29-12-2021
|
Let 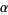 and
and 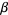 be any ordinal numbers, then ordinal exponentiation is defined so that if
be any ordinal numbers, then ordinal exponentiation is defined so that if 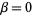 then
then 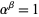 . If
. If 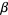 is not a limit ordinal, then choose
is not a limit ordinal, then choose 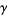 such that
such that 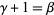 ,
,
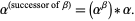 |
If 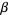 is a limit ordinal, then if
is a limit ordinal, then if 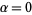 ,
, 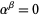 . If
. If 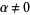 then,
then, 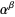 is the least ordinal greater than any ordinal in the set
is the least ordinal greater than any ordinal in the set 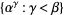 (Rubin 1967, p. 204; Suppes 1972, p. 215).
(Rubin 1967, p. 204; Suppes 1972, p. 215).
Note that this definition is not analogous to the definition for cardinals, since 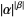 may not equal
may not equal 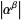 , even though
, even though 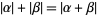 and
and 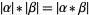 . Note also that
. Note also that 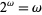 .
.
A familiar example of ordinal exponentiation is the definition of Cantor's first epsilon number. 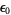 is the least ordinal such that
is the least ordinal such that 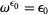 . It can be shown that it is the least ordinal greater than any ordinal in
. It can be shown that it is the least ordinal greater than any ordinal in 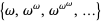 .
.
REFERENCES:
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|