المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Jacobi-Gauss Quadrature |
 446
 01:47 صباحاً
date: 5-12-2021 |
Author : Hildebrand, F. B 
Book or Source : Introduction to Numerical Analysis. New York: McGraw-Hill 
Page and Part : pp. 331-334|
Read More
Date: 8-12-2021
592
Date: 10-12-2021
935
Date: 2-12-2021
761
|
Jacobi-Gauss quadrature, also called Jacobi quadrature or Mehler quadrature, is a Gaussian quadrature over the interval ![[-1,1]](https://mathworld.wolfram.com/images/equations/Jacobi-GaussQuadrature/Inline1.gif)
with weighting function
 |
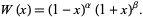(1) |
The abscissas for quadrature order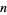 
are given by the roots of the Jacobi polynomials 
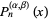. The weights are
 |
 |
 |
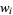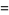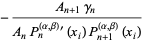(2) |
 |
 |
 |
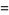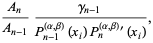(3) |
where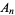 
is the coefficient of 
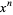in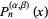 
. For Jacobi polynomials,
 |
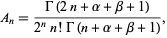(4) |
where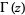 
is a gamma function. Additionally,
 |
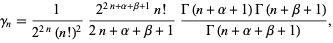(5) |
so
 |
 |
 |
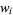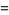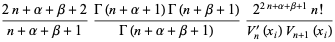(6) |
 |
 |
 |
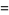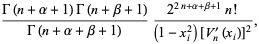(7) |
where
 |
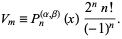(8) |
The error term is
![E_n=(Gamma(n+alpha+1)Gamma(n+beta+1)Gamma(n+alpha+beta+1))/((2n+alpha+beta+1)[Gamma(2n+alpha+beta+1)]^2)(2^(2n+alpha+beta+1)n!)/((2n)!)f^((2n))(xi)](https://mathworld.wolfram.com/images/equations/Jacobi-GaussQuadrature/NumberedEquation5.gif) |
(9) |
(Hildebrand 1956).
REFERENCES:
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 331-334, 1956.
|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|
