


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-8-2021
Date: 7-10-2021
Date: 14-11-2021
|
A recurrence plot is defined as a plot of the quantity
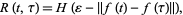 |
where 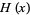 is the Heaviside step function and
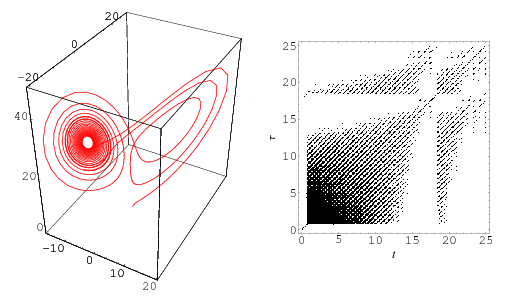
is the Heaviside step function and 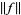 denotes a norm. A recurrence plot is therefore a binary plot. The figure above shows a recurrence plot for the Lorenz attractor with
denotes a norm. A recurrence plot is therefore a binary plot. The figure above shows a recurrence plot for the Lorenz attractor with 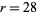 ,
, 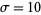 ,
, 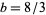 ,
, 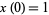 ,
, 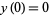 ,
, 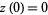 , and
, and 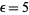 .
.
Recurrence plots were initially used to graphically display nonstationarity in time series (Eckmann et al. 1987, Gao and Cai 2000), but are also useful for visualizing functions.
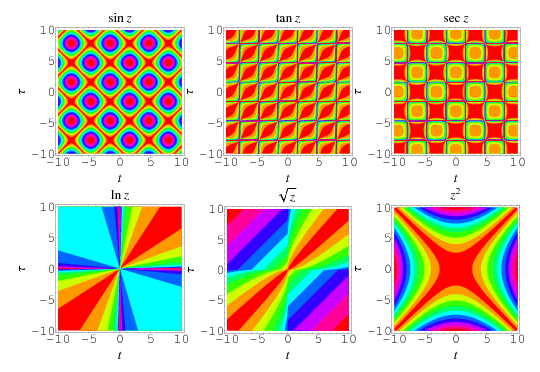
A so-called global recurrence plot or unthresholded recurrence plot of a function 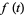 is a plot of
is a plot of 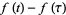 (or
(or 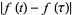 ) in the
) in the 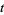 -
- plane. Recurrence plots for a number of common functions are illustrated above.
plane. Recurrence plots for a number of common functions are illustrated above.
REFERENCES:
Casdagli, M. C. "Recurrence Plots Revisited." Physica D 108, 12-44, 1997.
Eckmann, J. P.; Kamphorst, S. O.; and Ruelle, D. "Recurrence Plots of Dynamical Systems." Europhys. Lett. 4, 973-977, 1987.
Gao, J. and Cai, H. "On the Structures and Quantification of Recurrence Plots." Phys. Lett. A 270, 75-87, 2000.
Marwan, N. "Recurrence Plots and Cross Recurrence Plots." http://www.recurrence-plot.tk/.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 20, 2004. http://www.mathematicaguidebooks.org/.



|
|
|
|
باحثون يكشفون سببا غير متوقع وراء الصداع النصفي
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|