


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-11-2021
Date: 28-8-2021
Date: 26-8-2021
|

Rule 28 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation 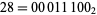 . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).
. This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).
The mirror image, complement, and mirror complement are rules 70, 199, and 157, respectively. For initial conditions consisting of a single black cell, it is equivalent to rule 156, since both have binary representations of the form 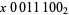 . The mirror image, complement, and mirrored complement of rule 156 are rules 198, 198, and 156, respectively (in other words, rule 156 is invariant under the combined complementing and mirror imaging operations).
. The mirror image, complement, and mirrored complement of rule 156 are rules 198, 198, and 156, respectively (in other words, rule 156 is invariant under the combined complementing and mirror imaging operations).
Starting with a single black cell, successive generations 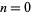 , 1, ... are given by interpreting the Jacobsthal numbers
, 1, ... are given by interpreting the Jacobsthal numbers 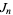 , namely 1, 3, 5, 11, 21, 43, 85, 171, 341, ... (OEIS A001045), in binary and ignoring leading zeros, namely 1, 11, 101, 1011, 10101, 101011, ... (OEIS A070909). Computation of the
, namely 1, 3, 5, 11, 21, 43, 85, 171, 341, ... (OEIS A001045), in binary and ignoring leading zeros, namely 1, 11, 101, 1011, 10101, 101011, ... (OEIS A070909). Computation of the 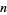 th generation is therefore computationally reducible for an initial configuration consisting of a single black cell by computing
th generation is therefore computationally reducible for an initial configuration consisting of a single black cell by computing
![a(n)=J_(n+2)=1/3[2^(n+2)-(-1)^n].](https://mathworld.wolfram.com/images/equations/Rule28/NumberedEquation1.gif) |
REFERENCES:
Sloane, N. J. A. Sequences A001045/M2482 and A070909 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 55, 90, and 952, 2002.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|