


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-7-2021
Date: 2-8-2021
Date: 21-7-2021
|
A topological space, also called an abstract topological space, is a set 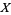 together with a collection of open subsets
together with a collection of open subsets 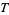 that satisfies the four conditions:
that satisfies the four conditions:
1. The empty set 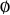 is in
is in 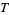 .
.
2. 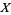 is in
is in 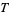 .
.
3. The intersection of a finite number of sets in 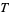 is also in
is also in 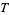 .
.
4. The union of an arbitrary number of sets in 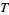 is also in
is also in 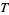 .
.
Alternatively,  may be defined to be the closed sets rather than the open sets, in which case conditions 3 and 4 become:
may be defined to be the closed sets rather than the open sets, in which case conditions 3 and 4 become:
3. The intersection of an arbitrary number of sets in  is also in
is also in  .
.
4. The union of a finite number of sets in  is also in
is also in  .
.
These axioms are designed so that the traditional definitions of open and closed intervals of the real line continue to be true. For example, the restriction in (3) can be seen to be necessary by considering  , where an infinite intersection of open intervals is a closed set.
, where an infinite intersection of open intervals is a closed set.
In the chapter "Point Sets in General Spaces" Hausdorff (1914) defined his concept of a topological space based on the four Hausdorff axioms (which in modern times are not considered necessary in the definition of a topological space).
REFERENCES:
Berge, C. Topological Spaces Including a Treatment of Multi-Valued Functions, Vector Spaces and Convexity. New York: Dover, 1997.
Hausdorff, F. Grundzüge der Mengenlehre. Leipzig, Germany: von Veit, 1914. Republished as Set Theory, 2nd ed. New York: Chelsea, 1962.
Munkres, J. R. Topology: A First Course, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|