


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-7-2021
Date: 13-6-2021
Date: 21-5-2021
|
The term "closure" has various meanings in mathematics.
The topological closure of a subset 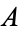 of a topological space
of a topological space 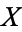 is the smallest closed subset of
is the smallest closed subset of 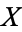 containing
containing 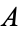 .
.
If 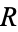 is a binary relation on some set
is a binary relation on some set 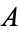 , then
, then 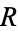 has reflexive, symmetric and transitive closures, each of which is the smallest relation on
has reflexive, symmetric and transitive closures, each of which is the smallest relation on 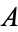 , with the indicated property, containing
, with the indicated property, containing 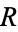 . Consequently, given any relation
. Consequently, given any relation 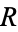 on any set
on any set 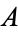 , there is always a smallest equivalence relation on
, there is always a smallest equivalence relation on 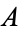 containing
containing 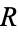 .
.
For some arbitrary property 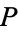 of relations, the relation
of relations, the relation 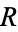 need not have a
need not have a 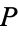 -closure, i.e., there need not be a smallest relation on
-closure, i.e., there need not be a smallest relation on 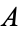 with the property
with the property 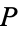 , and containing
, and containing 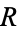 . For example, it often happens that a relation does not have an antisymmetric closure.
. For example, it often happens that a relation does not have an antisymmetric closure.
In algebra, the algebraic closure of a field 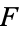 is a field
is a field 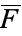 which can be said to be obtained from
which can be said to be obtained from 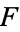 by adjoining all elements algebraic over
by adjoining all elements algebraic over 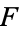 .
.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|