Completely Regular Space

A topological space 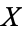 such that for every closed subset  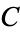of 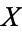 and every point 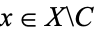, there is a continuous function  such that 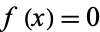 and .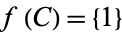

This is the definition given by most authors (Kelley 1955, p. 117; Willard 1970, pp. 94-95). However, some authors (e.g., Cullen 1968, p. 130) require the additional condition that 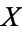 be a T1-space. In any case, every completely regular space is regular, and the converse is not true.

REFERENCES:

Cullen, H. F. "Normal Spaces. Completely Regular Spaces." §18 in Introduction to General Topology. Boston, MA: Heath, pp. 118-140, 1968.

Joshi, K. D. Introduction to General Topology. New Delhi, India: Wiley, p. 163, 1983.

Kelley, J. L. General Topology. New York: Van Nostrand, 1955.

Willard, S. "Regularity and complete regularity." §14 in General Topology. Reading, MA: Addison-Wesley, pp. 92-99, 1970.