المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Whitehead Link |
 1783
 06:28 مساءً
date: 28-6-2021 |
Author : Kauffman, L. 
Book or Source : Knots and Physics. Teaneck, NJ: World Scientific 
Page and Part : ...|
Read More
Date: 22-9-2016
1674
Date: 5-8-2021
1445
Date: 26-5-2021
1543
|
Whitehead Link
The prime link 05-0201, illustrated above, with braid word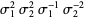 
or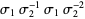 
and Jones polynomial
 |
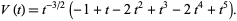The Whitehead link has linking number 0. It was discovered by Whitehead in 1934 (Whitehead 1962, pp. 21-50) as a counterexample to a piece of an attempted proof of the Poincaré conjecture (Milnor).
REFERENCES:
Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, p. 36, 1991.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 9 and 37-38, 1993.
Milnor, J. "The Poincaré Conjecture." https://www.claymath.org/millennium/Poincare_Conjecture/Official_Problem_Description.pdf.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 68, 72, and 137, 1976.
Whitehead, J. H. C. Mathematical Works, Vol. 2. London: Pergamon Press, pp. 21-50, 1962.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
