Square Knot

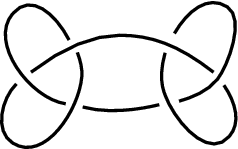
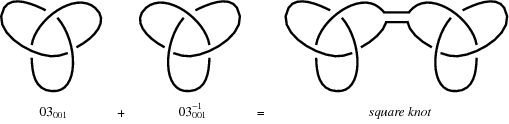
The square knot, also called the reef knot, is a composite knot of six crossings consisting of a knot sum of a trefoil knot and its mirror image (Rolfsen 1976, p. 220).

The square knot has the same Alexander polynomial 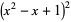 as the granny knot. It also has the same group as the granny knot (Rolfsen 1976, p. 62). However, the two knots are distinct. Fox (1952) showed that the knot complements of the square and granny knots are not homeomorphic (Rolfsen 1976, p. 62). In addition, the square knot is a slice knot, while the granny knot is not (Rolfsen 1976, p. 220).

The knot group of the square knot is

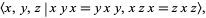which is isomorphic to that of the granny knot (Rolfsen 1976, p. 62).

REFERENCES:

Cipra, B. A. "To Have and Have Knot: When Are Knots Alike?" Science 241, 1291-1292, 1988.

Fox, R. H. "On the Complementary Domains of a Certain Pair of Inequivalent Knots." Proc. Kon. Nederl. Akad. Wetensch. Ser. A 55, 37-40, 1952.

Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, pp. 6, 8, and 327, 1991.

Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 38-39, 1993.

Owen, P. Knots. Philadelphia, PA: Courage, p. 50, 1993.

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 40, 61, and 220, 1976.