Prime Knot

A knot is called prime if, for any decomposition as a connected sum, one of the factors is unknotted (Livingston 1993, pp. 5 and 78). A knot which is not prime is called a composite knot. It is often possible to combine two prime knots to create two different composite knots, depending on the orientation of the two. Schubert (1949) showed that every knot can be uniquely decomposed (up to the order in which the decomposition is performed) as a knot sum of prime knots.

In general, it is nontrivial to determine if a given knot is prime or composite (Hoste et al. 1998). However, in the case of alternating knots, Menasco (1984) showed that a reduced alternating diagram represents a prime knot iff the diagram is itself prime ("an alternating knot is prime iff it looks prime"; Hoste et al. 1998).

There is no known formula for giving the number of distinct prime knots as a function of the number of crossings. The numbers of distinct prime knots having 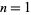, 2, ... crossings are 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, ... (OEIS A002863). A pictorial enumeration of prime knots of up to 10 crossings appears in Rolfsen (1976, Appendix C). Note, however, that in this table, the Perko pair 10-161 and 10-162 are actually identical, and the uppermost crossing in 10-144 should be changed (Jones 1987). The 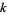th knot having  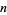crossings in this (arbitrary) ordering of knots is given the symbol 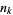. The following table summarizes a number of named prime knots.

knot symbol	prime knot
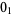	unknot
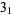	trefoil knot
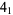	figure eight knot
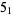	Solomon's seal knot
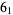	stevedore's knot
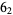	Miller Institute knot
--	Conway's knot
--	Kinoshita-Terasaka knot

Thistlethwaite has used Dowker notation to enumerate the number of prime knots of up to 13 crossings. In this compilation, mirror images are counted as a single knot type. Hoste et al. (1998) subsequently tabulated all prime knots up to 16 crossings. Hoste and Weeks subsequently began compiling a list of 17-crossing prime knots (Hoste et al. 1998).

Let 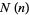 be the number of distinct prime knots with  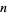crossings, counting chiral versions of the same knot separately. Then

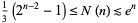(Ernst and Summers 1987). Welsh has shown that the number of knots is bounded by an exponential in 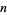, and it is also known that

(Welsh 1991, Hoste et al. 1998, Thistlethwaite 1998).

REFERENCES:

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 8-9, 1994.

Burde, G. and Zieschang, H. Knots, 2nd rev. ed. Berlin: de Gruyter, 2002.

Ernst, C. and Sumners, D. W. "The Growth of the Number of Prime Knots." Math. Proc. Cambridge Philos. Soc. 102, 303-315, 1987.

Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 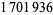 Knots." Math. Intell. 20, 33-48, Fall 1998.

Jones, V. F. R. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.

Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 9 and 78, 1993.

Menasco, W. "Closed Incompressible Surfaces in Alternating Knot and Link Complements." Topology 23, 37-44, 1984.

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 335, 1976.

Schubert, H. Sitzungsber. Heidelberger Akad. Wiss., Math.-Naturwiss. Klasse, 3rd Abhandlung. 1949.

Sloane, N. J. A. Sequence A002863/M0851 in "The On-Line Encyclopedia of Integer Sequences."

Sloane, N. J. A. and Plouffe, S. Figure M0851 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Thistlethwaite, M. "On the Structure and Scarcity of Alternating Links and Tangles." J. Knot Th. Ramifications 7, 981-1004, 1998.

Welsh, D. J. A. "On the Number of Knots and Links." Colloq. Math. Soc. J. Bolyai 60, 713-718, 1991.