


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-5-2021
Date: 17-7-2021
Date: 17-5-2021
|
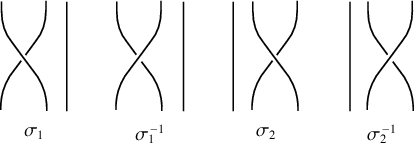
A braid is an intertwining of some number of strings attached to top and bottom "bars" such that each string never "turns back up." In other words, the path of each string in a braid could be traced out by a falling object if acted upon only by gravity and horizontal forces. A given braid may be assigned a symbol known as a braid word that uniquely identifies it (although equivalent braids may have more than one possible representations). In particular, an 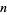 -braid can constructed by iteratively applying the
-braid can constructed by iteratively applying the 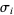 (
(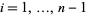 ) operator, which switches the lower endpoints of the
) operator, which switches the lower endpoints of the 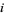 th and
th and 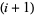 th strings--keeping the upper endpoints fixed--with the
th strings--keeping the upper endpoints fixed--with the 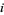 th string brought above the
th string brought above the 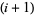 th string. If the
th string. If the 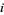 th string passes below the
th string passes below the 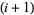 th string, it is denoted
th string, it is denoted 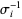 .
.

An ordered combination of the 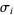 and
and 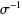 symbols constitutes a braid word. For example,
symbols constitutes a braid word. For example, 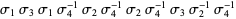 is a braid word for the braid illustrated above, where the symbols can be read off the diagram left to right and then top to bottom.
is a braid word for the braid illustrated above, where the symbols can be read off the diagram left to right and then top to bottom.
By Alexander's theorem, any link is representable by a closed braid, but there is no general procedure for reducing a braid word to its simplest form. However, Markov's theorem gives a procedure for identifying different braid words which represent the same link.
The following table lists (not necessarily unique) braid words for some common knots and links.
| link | braid word |
| Borromean rings | 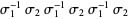 |
| figure eight knot | 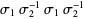 |
| Hopf link | 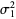 |
| Miller Institute knot | 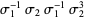 |
| Solomon's seal knot | 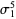 |
| stevedore's knot | 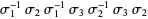 |
| trefoil knot | 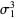 |
| Whitehead link | 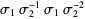 |
Let 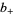 be the sum of positive exponents, and
be the sum of positive exponents, and 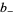 the sum of negative exponents in the braid group
the sum of negative exponents in the braid group 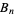 . If
. If
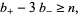 |
then the closed braid 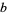 is not amphichiral (Jones 1985).
is not amphichiral (Jones 1985).
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 132-133, 1994.
Jones, V. F. R. "A Polynomial Invariant for Knots via von Neumann Algebras." Bull. Amer. Math. Soc. 12, 103-111, 1985.
Jones, V. F. R. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.
Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|