


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-6-2021
Date: 22-6-2021
Date: 21-6-2017
|
A smooth structure on a topological manifold (also called a differentiable structure) is given by a smooth atlas of coordinate charts, i.e., the transition functions between the coordinate charts are 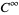 smooth. A manifold with a smooth structure is called a smooth manifold (or differentiable manifold).
smooth. A manifold with a smooth structure is called a smooth manifold (or differentiable manifold).
A smooth structure is used to define differentiability for real-valued functions on a manifold. This extends to a notion of when a map between two differentiable manifolds is smooth, and naturally to the definition of a diffeomorphism. In addition, the smooth structure is used to define manifold tangent vectors, the collection of which is the tangent bundle.
Two smooth structures are considered equivalent if there is a homeomorphism of the manifold which pulls back one atlas to an atlas compatible to the other one, i.e., a diffeomorphism. For instance, any two smooth structures on the circle 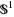 are equivalent, as can be seen by integration.
are equivalent, as can be seen by integration.
It is surprising that some manifolds admit more than one smooth structure. The first such example was an exotic sphere of 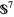 , the seven-dimensional hypersphere, found by Milnor (1956) using the calculus of octonions. In the 1980s, several mathematicians, including Casson, Freedman, and Donaldson, showed that four-dimensional Euclidean space
, the seven-dimensional hypersphere, found by Milnor (1956) using the calculus of octonions. In the 1980s, several mathematicians, including Casson, Freedman, and Donaldson, showed that four-dimensional Euclidean space 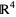 has smooth structures that are distinct from the standard structure. These are called exotic R4s, and some of their techniques involve Donaldson theory.
has smooth structures that are distinct from the standard structure. These are called exotic R4s, and some of their techniques involve Donaldson theory.
Another approach to smooth structures is through topological sheaf theory. Notice that a coordinate chart for an 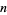 -dimensional manifold is really an ordered collection of
-dimensional manifold is really an ordered collection of 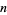 continuous functions. Whenever two coordinate charts overlap on the manifold, the functions from one chart are infinitely differentiable with respect to those from the other chart. The collection of compatible real-valued continuous functions defines the sheaf of smooth functions. Conversely, one can define a smooth structure to be defined by a subsheaf of continuous functions which satisfies the mutually differentiable condition.
continuous functions. Whenever two coordinate charts overlap on the manifold, the functions from one chart are infinitely differentiable with respect to those from the other chart. The collection of compatible real-valued continuous functions defines the sheaf of smooth functions. Conversely, one can define a smooth structure to be defined by a subsheaf of continuous functions which satisfies the mutually differentiable condition.
REFERENCES:
Milnor, J. "On Manifolds Homeomorphic to the 7-Sphere." Ann. Math. 64, 399-405, 1956.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|