


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-3-2021
Date: 4-5-2021
Date: 14-4-2021
|
There are essentially three types of Fisher-Tippett extreme value distributions. The most common is the type I distribution, which are sometimes referred to as Gumbel types or just Gumbel distributions. These are distributions of an extreme order statistic for a distribution of 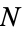 elements
elements 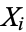 .
.
The Fisher-Tippett distribution corresponding to a maximum extreme value distribution (i.e., the distribution of the maximum 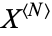 ), sometimes known as the log-Weibull distribution, with location parameter
), sometimes known as the log-Weibull distribution, with location parameter 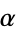 and scale parameter
and scale parameter 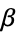 is implemented in the Wolfram Language as ExtremeValueDistribution[alpha, beta].
is implemented in the Wolfram Language as ExtremeValueDistribution[alpha, beta].
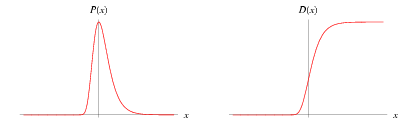
It has probability density function and distribution function
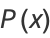 |
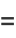 |
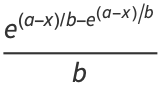 |
(1) |
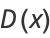 |
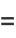 |
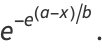 |
(2) |
The moments can be computed directly by defining
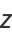 |
 |
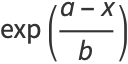 |
(3) |
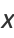 |
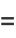 |
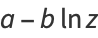 |
(4) |
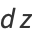 |
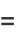 |
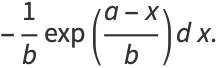 |
(5) |
Then the raw moments are
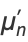 |
 |
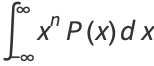 |
(6) |
 |
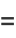 |
![1/bint_(-infty)^inftyx^nexp((a-x)/b)exp[-e^((a-x)/b)]dx](https://mathworld.wolfram.com/images/equations/ExtremeValueDistribution/Inline26.gif) |
(7) |
 |
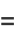 |
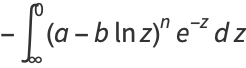 |
(8) |
 |
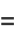 |
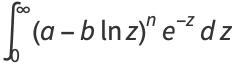 |
(9) |
 |
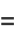 |
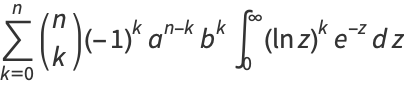 |
(10) |
 |
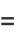 |
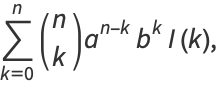 |
(11) |
where 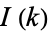 are Euler-Mascheroni integrals. Plugging in the Euler-Mascheroni integrals
are Euler-Mascheroni integrals. Plugging in the Euler-Mascheroni integrals 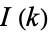 gives
gives
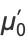 |
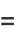 |
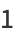 |
(12) |
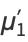 |
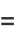 |
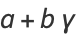 |
(13) |
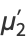 |
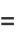 |
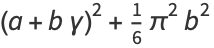 |
(14) |
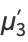 |
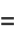 |
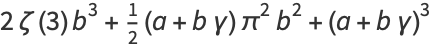 |
(15) |
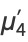 |
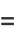 |
![a^4+4a^3bgamma+6a^2b^2(gamma^2+1/6pi^2)+4ab^3[gamma^3+1/2gammapi^2+2zeta(3)]+b^4[gamma^4+gamma^2pi^2+3/(20)pi^4+8gammazeta(3)],](https://mathworld.wolfram.com/images/equations/ExtremeValueDistribution/Inline55.gif) |
(16) |
where 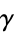 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 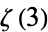 is Apéry's constant.
is Apéry's constant.
The corresponding central moments are therefore
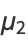 |
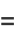 |
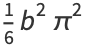 |
(17) |
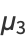 |
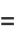 |
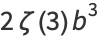 |
(18) |
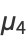 |
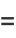 |
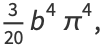 |
(19) |
giving mean, variance, skewness, and kurtosis excess of
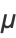 |
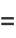 |
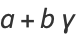 |
(20) |
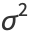 |
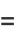 |
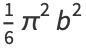 |
(21) |
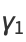 |
 |
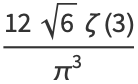 |
(22) |
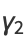 |
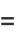 |
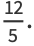 |
(23) |
The characteristic function is
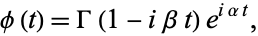 |
(24) |
where 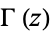 is the gamma function (Abramowitz and Stegun 1972, p. 930).
is the gamma function (Abramowitz and Stegun 1972, p. 930).
An analog to the central limit theorem states that the asymptotic normalized distribution of 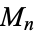 satisfies one of the three distributions
satisfies one of the three distributions
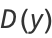 |
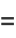 |
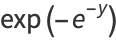 |
(25) |
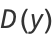 |
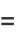 |
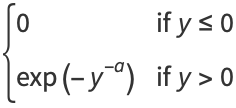 |
(26) |
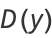 |
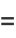 |
![{exp[-(-y)^a] if y<=0; 1 if y>0,](https://mathworld.wolfram.com/images/equations/ExtremeValueDistribution/Inline89.gif) |
(27) |
also known as Gumbel-type, Fréchet-type, and Weibull-type distributions, respectively.
The distributions of 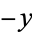 are also extreme value distributions. The Gumbel-type distribution for
are also extreme value distributions. The Gumbel-type distribution for 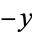 is implemented in as GumbelDistribution[alpha, beta]. The Weibull-type distribution for
is implemented in as GumbelDistribution[alpha, beta]. The Weibull-type distribution for 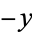 is a Weibull distribution. The two-parameter Weibull distribution is implemented as WeibullDistribution[alpha, beta].
is a Weibull distribution. The two-parameter Weibull distribution is implemented as WeibullDistribution[alpha, beta].
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Balakrishnan, N. and Cohen, A. C. Order Statistics and Inference. New York: Academic Press, 1991.
David, H. A. Order Statistics, 2nd ed. New York: Wiley, 1981.
Finch, S. R. "Extreme Value Constants." §5.16 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 363-367, 2003.
Gibbons, J. D. and Chakraborti, S. (Eds.). Nonparametric Statistical Inference, 3rd rev. ext. ed. New York: Dekker, 1992.
Johnson, N.; Kotz, S.; and Balakrishnan, N. Continuous Univariate Distributions, Vol. 2, 2nd ed. New York: Wiley, 1995.
Natrella, M. "Extreme Value Distributions." §8.1.6.3 in Engineering Statistics Handbook. NIST/SEMATECH, 2005. https://www.itl.nist.gov/div898/handbook/apr/section1/apr163.htm.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|