


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 9-3-2016
Date: 13-5-2017
Date: 23-3-2021
|
Relation to Rayleigh–Schr¨odinger Perturbation Theory
The Rayleigh–Schr¨odinger version of perturbation theory determines the part of the perturbed state parallel to | ψ〉0, by insisting that | ψ〉0 + |Φ〉RS have length one. Thus,
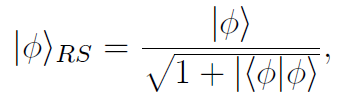
where |Φ〉 is the BW state. It is a lot easier to compute the normalized eigenstate from this formula than to apply the RS rules directly.
There is another aspect of the difference between the two methods of computing the perturbation expansion which is exposed by the above formula. A perturbative calculation of |Φ〉 gives an infinite number of powers of g in the normalized wave function. Similarly, if we write the expression for the energy in BW perturbation theory
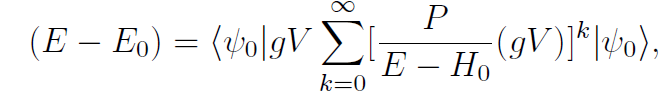
then at a finite order in the expansion, we get a nonlinear equation for E, whose exact solution contains an infinite number of powers of g. There has not been much exploration of whether the resummations of perturbation theory implicit in the BW formalism lead to better approximations at finite values of g.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم الهدايا والنذور يوضح آلية العثور على مفقودات الزائرين وطريقة استعادتها
|
|
|