


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-2-2021
Date: 14-2-2021
Date: 25-4-2021
|
Given a statistical distribution with measured mean, mode, and standard deviation 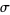 , the Pearson mode skewness is
, the Pearson mode skewness is
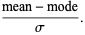 |
The function was incorrectly implemented (with a spurious multiplicative factor of 3) in versions of the Wolfram Language prior to 6 as PearsonSkewness1[data] after loading the package Statistics`DescriptiveStatistics`.
This measure was suggested by Karl Pearson, and has the property that for a type III Pearson distribution, it is equal to
 |
where 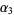 is the third standardized moment (Kenney and Keeping 1962, p. 101; Kenney and Keeping 1951, p. 106).
is the third standardized moment (Kenney and Keeping 1962, p. 101; Kenney and Keeping 1951, p. 106).
REFERENCES:
Hildebrand, D. K. Statistical Thinking for Behavioral Scientists. Boston: Duxbury, 1986.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, p. 101, 1962.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, p. 106, 1951.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
قسم التربية والتعليم ينهي استعداداته الخاصة بالحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|