Kurtosis

Kurtosis is defined as a normalized form of the fourth central moment 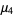 of a distribution. There are several flavors of kurtosis, the most commonly encountered variety of which is normally termed simply "the" kurtosis and is denoted  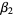(Pearson's notation; Abramowitz and Stegun 1972, p. 928) or  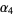(Kenney and Keeping 1951, p. 27; Kenney and Keeping 1961, pp. 99-102). The kurtosis of a theoretical distribution is defined by

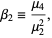(1)

where 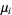 denotes the 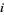th central moment (and in particular,  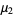is the variance). This form is implemented in the Wolfram Language as Kurtosis[dist].

The "kurtosis excess" (Kenney and Keeping 1951, p. 27) is defined by

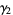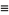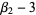			(2)
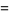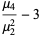			(3)

and is commonly denoted 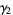 (Abramowitz and Stegun 1972, p. 928) or 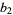. Kurtosis excess is commonly used because  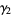of a normal distribution is equal to 0, while the kurtosis proper is equal to 3. Unfortunately, Abramowitz and Stegun (1972) confusingly refer to  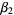as the "excess or kurtosis."

For many distributions encountered in practice, a positive 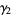 corresponds to a sharper peak with higher tails than if the distribution were normal (Kenney and Keeping 1951, p. 54). This observation is likely the reason kurtosis excess was historically (but incorrectly) regarded as a measure of the "peakedness" of a distribution. However, the correspondence between kurtosis and peakedness is not true in general; in fact, a distribution with a perfectly flat top may have infinite kurtosis, while one with infinite peakedness may have negative kurtosis excess. As a result, kurtosis excess provides a measure of outliers (i.e., the presence of "heavy tails") in a distribution, not its degree of peakedness (Kaplansky 1945; Kenney and Keeping 1951, p. 27; Westfall 2014).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 928, 1972.

Darlington, R. B. "Is Kurtosis Really Peakedness?" Amer. Statist. 24, 19-22, 1970.

Dodge, Y. and Rousson, V. "The Complications of the Fourth Central Moment." Amer. Statist. 53, 267-269, 1999.

Kaplansky, I. "A Common Error Concerning Kurtosis." J. Amer. Stat. Assoc. 40, 259, 1945.

Kenney, J. F. and Keeping, E. S. "Kurtosis." §7.12 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 102-103, 1962.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.

Moors, J. J. A. "The Meaning of Kurtosis: Darlington Reexamined." Amer. Statist. 40, 283-284, 1986.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Moments of a Distribution: Mean, Variance, Skewness, and So Forth." §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.

Ruppert, D. "What is Kurtosis? An Influence Function Approach." Amer. Statist. 41, 1-5, 1987.

Westfall, P. H. "Kurtosis as Peakedness, 1905-2014. R.I.P." Amer. Statist. 68, 191-195, 2014.