


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2020
Date: 21-12-2019
Date: 12-2-2020
|
A Sierpiński number of the first kind is a number of the form 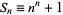 . The first few are 2, 5, 28, 257, 3126, 46657, 823544, 16777217, ... (OEIS A014566). Sierpiński proved that if
. The first few are 2, 5, 28, 257, 3126, 46657, 823544, 16777217, ... (OEIS A014566). Sierpiński proved that if 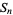 is prime with
is prime with 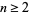 , then
, then 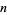 must be of the form
must be of the form 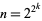 , making
, making 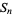 a Fermat number
a Fermat number 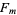 with
with 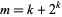 . The first few
. The first few 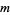 of this form are 1, 3, 6, 11, 20, 37, 70, ... (OEIS A006127).
of this form are 1, 3, 6, 11, 20, 37, 70, ... (OEIS A006127).
The numbers of digits in the number 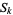 is given by
is given by
![d_k=[2^(k+2^k)log_(10)2],](https://mathworld.wolfram.com/images/equations/SierpinskiNumberoftheFirstKind/NumberedEquation1.gif) |
where ![[z]](https://mathworld.wolfram.com/images/equations/SierpinskiNumberoftheFirstKind/Inline11.gif) is the ceiling function, so the numbers of digits in the first few candidates are 1, 3, 20, 617, 315653, 41373247568, ... (OEIS A089943).
is the ceiling function, so the numbers of digits in the first few candidates are 1, 3, 20, 617, 315653, 41373247568, ... (OEIS A089943).
The only known prime Sierpiński numbers of the first kind are 2, 5, 257, with the first unknown case being 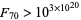 . The status of Sierpiński numbers is summarized in the table below (Nielsen).
. The status of Sierpiński numbers is summarized in the table below (Nielsen).
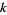 |
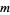 |
status of 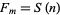 |
| 0 | 1 | prime (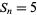 ) ) |
| 1 | 3 | prime (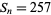 ) ) |
| 2 | 6 | composite with factor 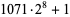 |
| 3 | 11 | composite with factor 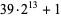 |
| 4 | 20 | composite with no factor known |
| 5 | 37 | composite with factor 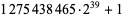 |
| 6 | 70 | unknown |
| 7 | 135 | unknown |
| 8 | 264 | unknown |
| 9 | 521 | unknown |
| 10 | 1034 | unknown |
| 11 | 2059 | composite with factor 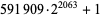 |
| 12 | 4108 | unknown |
| 13 | 8205 | unknown |
| 14 | 16398 | unknown |
| 15 | 32783 | unknown |
| 16 | 65552 | unknown |
| 17 | 131089 | unknown |
REFERENCES:
Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 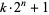 ." Math. Comput. 41, 661-673, 1983.
." Math. Comput. 41, 661-673, 1983.
Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 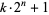 , II." In prep.
, II." In prep.
Keller, W. "Prime Factors 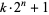 of Fermat Numbers
of Fermat Numbers 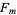 and Complete Factoring Status." https://www.prothsearch.net/fermat.html.
and Complete Factoring Status." https://www.prothsearch.net/fermat.html.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 155, 1979.
Nielsen, J. S. "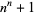 ." https://jeppesn.dk/nton.html.
." https://jeppesn.dk/nton.html.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 74, 1989.
Sloane, N. J. A. Sequences A006127/M2547, A014566, A089943 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|