
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-10-2019
Date: 6-4-2020
Date: 20-11-2020
|
The pentanacci numbers are a generalization of the Fibonacci numbers defined by 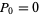 ,
, 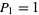 ,
, 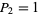 ,
, 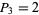 ,
, 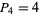 , and the recurrence relation
, and the recurrence relation
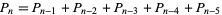 |
(1) |
for 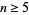 . They represent the
. They represent the 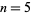 case of the Fibonacci n-step numbers.
case of the Fibonacci n-step numbers.
The first few terms for 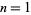 , 2, ... are 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, ... (OEIS A001591).
, 2, ... are 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, ... (OEIS A001591).
The ratio of adjacent terms tends to the real root of 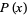 , namely 1.965948236645485... (OEIS A103814), sometimes called the pentanacci constant.
, namely 1.965948236645485... (OEIS A103814), sometimes called the pentanacci constant.
An exact formula for the 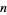 th pentanacci number can be given explicitly in terms of the five roots
th pentanacci number can be given explicitly in terms of the five roots 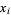 of
of
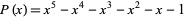 |
(2) |
as
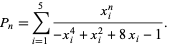 |
(3) |
The pentanacci numbers have generating function
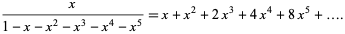 |
(4) |
REFERENCES:
Sloane, N. J. A. Sequence A001591/M1122 and A103814 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|