


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 30-11-2020
Date: 15-12-2016
Date: 28-12-2016
|
Spacial Frequency k
When we let a traveling wave pass by us, we observe a sinusoidal oscillation in time. This oscillation can be described in terms of the number of seconds in each cycle (T seconds/cycle), in terms of the frequency (f cycles/second) or the angular frequency (ω radians/second) .
If instead we look at the whole wave at one instant of time, or move along with the wave, we see a sinusoidal oscillation in space. We have described this spacial oscillation in terms of the wavelength, the number of meters in each cycle (λ meters/cycle). What we are missing is a spacial analogy to frequency, the number of cycles or radians per meter.
By dimensions we immediately see that
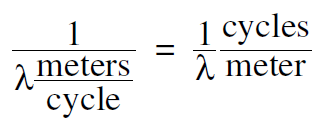
is the special analogy to the time frequency f, and that
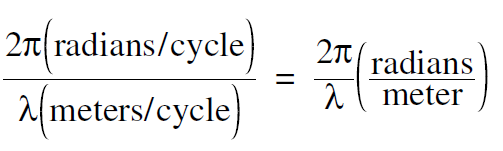
is the spacial analogy to the angular frequency ω .
In physics texts, it is not common to use a special symbol to designate the spacial frequency 1/ λ (cycles/meter), but it is standard practice to designate the angular spacial frequency 2π /λ (radians/meter) by the letter k
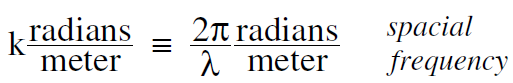 ........(1)
........(1)
The standard name for k is the lackluster expression wave number, which says very little about the quantity. Instead we will refer to k as the spacial frequency of the wave. The higher the spacial frequency k, the more radians we get in a meter, just as the higher the time frequency ω , the more radians we get in one second. When you first study wave motion, it may be an irritating complication to have two kinds of frequency, f cycles/sec and ω radians/sec (or two spacial frequencies 1/ λ cycles/meter and k radians/meter). Why not stick with cycles which are much easier to visualize than radians? The answer is that in the formulas for sine waves, the sine function basically has to be expressed in terms of an angle, as in sin θ , and radians are an angle. To convert time t to an angle, we multiply by ω as in
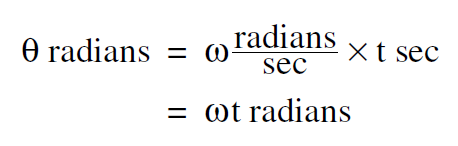 ..........(2a)
..........(2a)
while to convert the distance x to an angle we multiply by k as in
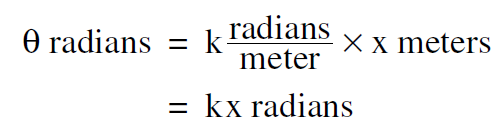 ..........(2b)
..........(2b)
Using Equations 2a or 2b, we can express the single function sin θ either as sin ωt , a sine wave in time shown in Figure (1a), or as sin kx, a sine wave in space shown in Figure (1b). From these graphs we can see that when ωt gets up to 2π , we have one period T, and when kx gets up to 2π we have one wavelength λ .
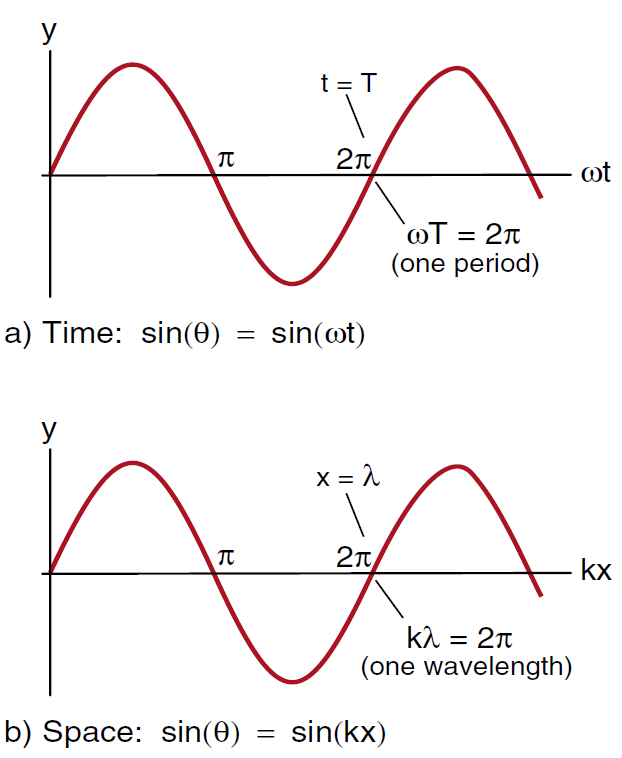
Figure 1: Sine waves in time and space.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|