


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-10-2020
Date: 14-3-2020
Date: 9-9-2020
|
A number (usually base 10 unless specified otherwise) which has no digitaddition generator. Such numbers were originally called Colombian numbers (S. 1974). There are infinitely many such numbers, since an infinite sequence of self numbers can be generated from the recurrence relation
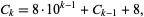 |
(1) |
for 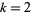 , 3, ..., where
, 3, ..., where 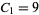 . The first few self numbers are 1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97, ... (OEIS A003052).
. The first few self numbers are 1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97, ... (OEIS A003052).
An infinite number of 2-self numbers (i.e., base-2 self numbers) can be generated by the sequence
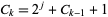 |
(2) |
for 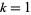 , 2, ..., where
, 2, ..., where 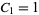 and
and 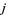 is the number of digits in
is the number of digits in 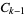 . An infinite number of
. An infinite number of 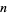 -self numbers can be generated from the sequence
-self numbers can be generated from the sequence
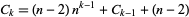 |
(3) |
for 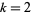 , 3, ..., and
, 3, ..., and
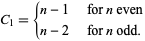 |
(4) |
Joshi (1973) proved that if 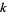 is odd, then
is odd, then 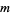 is a
is a 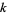 -self number iff
-self number iff 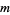 is odd. Patel (1991) proved that
is odd. Patel (1991) proved that 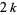 ,
, 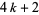 , and
, and 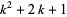 are
are 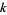 -self numbers in every even base
-self numbers in every even base 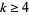 .
.
REFERENCES:
Cai, T. "On 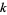 -Self Numbers and Universal Generated Numbers." Fib. Quart. 34, 144-146, 1996.
-Self Numbers and Universal Generated Numbers." Fib. Quart. 34, 144-146, 1996.
Gardner, M. Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 115-117, 122, 1988.
Joshi, V. S. Ph.D. dissertation. Gujarat University, Ahmadabad, 1973.
Kaprekar, D. R. The Mathematics of New Self-Numbers. Devaiali, pp. 19-20, 1963.
Patel, R. B. "Some Tests for 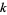 -Self Numbers." Math. Student 56, 206-210, 1991.
-Self Numbers." Math. Student 56, 206-210, 1991.
S., B. R. "Solution to Problem E 2048." Amer. Math. Monthly 81, 407, 1974.
Sloane, N. J. A. Sequence A003052/M2404 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|