There are two related conjectures, each called the twin prime conjecture. The first version states that there are an infinite number of pairs of twin primes (Guy 1994, p. 19). It is not known if there are an infinite number of such primes (Wells 1986, p. 41; Shanks 1993, p. 30), but it seems almost certain to be true. While Hardy and Wright (1979, p. 5) note that "the evidence, when examined in detail, appears to justify the conjecture," and Shanks (1993, p. 219) states even more strongly, "the evidence is overwhelming," Hardy and Wright also note that the proof or disproof of conjectures of this type "is at present beyond the resources of mathematics."

Arenstorf (2004) published a purported proof of the conjecture (Weisstein 2004). Unfortunately, a serious error was found in the proof. As a result, the paper was retracted and the twin prime conjecture remains fully open.

The conjecture that there are infinitely many Sophie Germain primes, i.e., primes 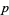 such that  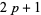is also prime, is very closely related (Shanks 1993, p. 30).

A second twin prime conjecture states that adding a correction proportional to 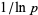 to a computation of Brun's constant ending with  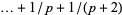will give an estimate with error less than 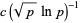. An extended form of this conjecture, sometimes called the strong twin prime conjecture (Shanks 1993, p. 30) or first Hardy-Littlewood conjecture, states that the number  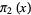of twin primes  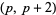less than or equal to  is asymptotically equal to

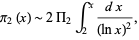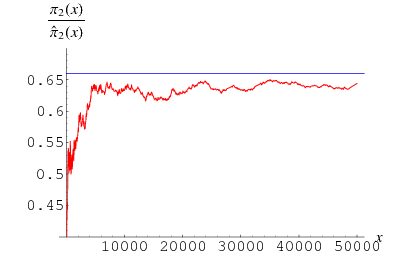
where 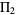 is the so-called twin primes constant (Hardy and Littlewood 1923). The value of  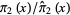is plotted above for 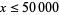, with  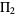indicated in blue and taking .

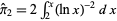This conjecture is a special case of the more general k-tuple conjecture (also known as the first Hardy-Littlewood conjecture), which corresponds to the set {0,2}" src="https://mathworld.wolfram.com/images/equations/TwinPrimeConjecture/Inline14.gif" style="height:15px; width:57px" />.

REFERENCES:

Arenstorf, R. F. "There Are Infinitely Many Prime Twins." 26 May 2004. https://arxiv.org/abs/math.NT/0405509.

Guy, R. K. "Gaps between Primes. Twin Primes." §A8 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 19-23, 1994.

Hardy, G. H. and Littlewood, J. E. "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes." Acta Math. 44, 1-70, 1923.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 30-31, 2003.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 261-265, 1996.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 30, 1993.

Tenenbaum, G. "Re: Arenstorf's paper on the Twin Prime Conjecture." 8 Jun 2004. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0406&L=nmbrthry&F=&S=&P=1119.

Weisstein, E. W. "Twin Prime Proof Proffered." MathWorld headline news, June 9, 2004. https://mathworld.wolfram.com/news/2004-06-09/twinprimes/.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 41, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد